[BOJ알고리즘, C++]#2263_트리의 순회
BOJ 알고리즘 문제 풀이, 2263번 문제 "트리의 순회"
트리의 순회 방법에 대해 공부하고, 후위순회와 중위순회를 통해 전위순회를 구하는 방법
Overview
- 문제
- 풀이
- 코드
#1. 문제
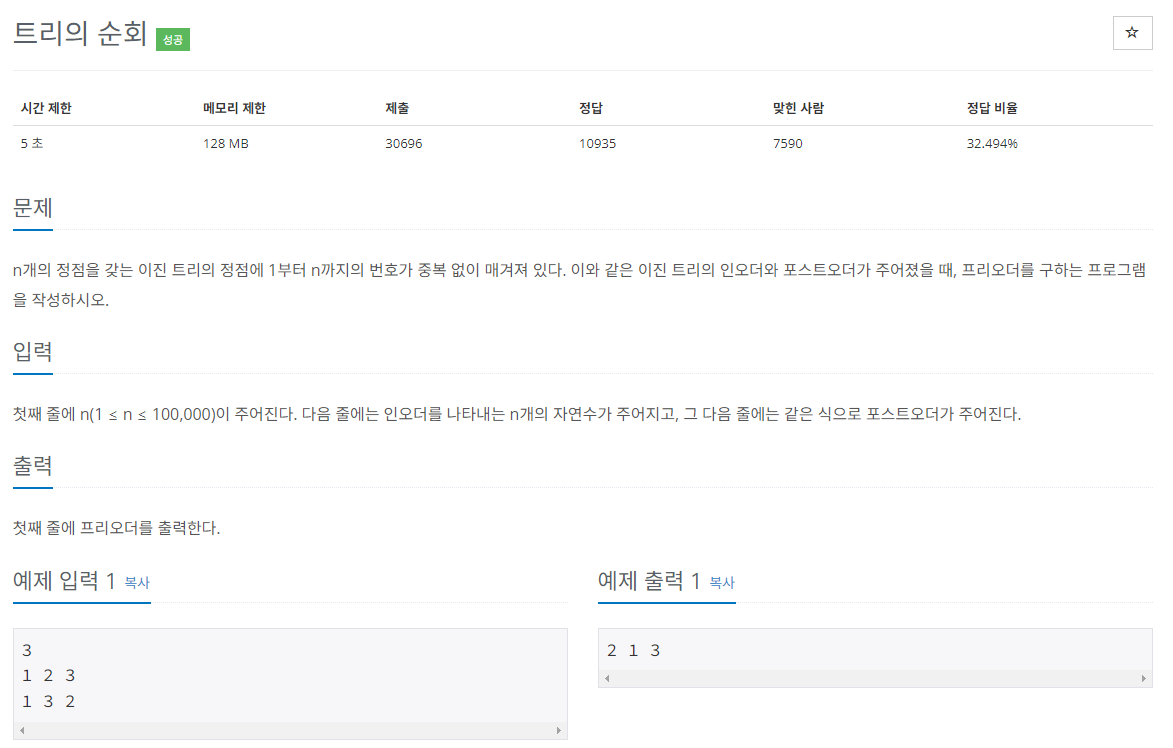
#2. 풀이
1. 트리
[자료구조]#5_트리
[자료구조]#5_트리 트리 자료구조에 대해 알아보겠습니다. Overview 개념 이진트리 순회 이진 탐색 트리 균형 이진트리 AVL 트리 레드-블랙 트리 Map, Set 힙 #0. 개념 1. 트리? [정의] : 트리는 1:n 관계의
webddevys.tistory.com
- [정의] : 트리는 1:n 관계의 계층 구조를 갖는 비 선형 자료구조입니다. 트리는 노드와 노드 간 연결관계를 표현하는 간선으로 이루어져 있습니다.
- [특징] : 트리의 두 가지 주요 특징은 계층 구조와 비순환 구조입니다. 트리의 노드는 부모-자식 관계 갖고 계층구조를 형성하며, 순환 구조를 갖지 않습니다.
2. 트리의 순회
- [개념] : 트리의 순회는 모든 노드를 탐색 할 때, 세 가지 방문 순서에 기반합니다.
- [종류]
- 전위순회(Preorder) : 부모 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드
- 중위순회(Inorder) : 왼쪽 자식 노드 -> 부모 노드 -> 오른쪽 자식 노드
- 후위순회(Postorder) : 왼쪽 자식 노드 -> 오른쪽 노드 -> 부모 노드
3. 후위순회와 중위순회를 통해 '부모', '왼쪽 자식 노드', '오른쪽 자식 노드' 정보 찾기
중위 순회 = '1 2 3'
후위 순회 = '1 3 2'
// 후위순회 내 마지막 노드가 트리의 루트 노드다
1. 트리의 루트 노드 = 후위순회[후위순회.size()-1] = '2'
// 중위순회 내 루트노드의 위치를 기준으로 왼쪽과 오른쪽 서브트리를 분할한다.
2. 중위 순회 내 루트 노드의 위치 = '1 [2] 3'
3. 중위 순회 내 루트 노드 기준 왼쪽 서브트리 = '[1] 2 3'
4. 중위 순회 내 루트 노드 기준 오른쪽 서브트리 = '1 2 [3]'
// 위 과정을 재귀적으로 수행한다.
1. 루트 노드 출력
2. 왼쪽 서브트리에 대해 재귀호출 수행
-> findPreorder(in_start, position[root]-1,
post_start, post_start + (position[root]-1-in_start));
-> 2-1. 중위순회 내 현재 부모 노드 기준 왼쪽 서브트리는 부모 노드 기준 왼쪽에 있는 노드들이다.
-> 2-2. 후위순회 내 현재 부모 노드 기준 왼쪽 서브트리는 중위순회 내 왼쪽 서브트리 노드들의 개수만큼
후위순회의 시작점부터 해당 개수만큼의 노드들이다.
3. 오른쪽 서브트리에 대한 재귀호출 수행
-> findPreorder(position[root]+1, in_end,
post_start+(position[root]-in_start), post_end-1);
-> 3-1. 중위순회 내 현재 부모 노드 기준 오른쪽 서브트리는 부모 노드 기준 왼쪽에 있는 모든 노드들이다.
-> 3-2. 후위순회 내 현재 부모 노드 기준 오른쪽 서브트리는 중위순회 내 오른쪽 서브트리 노드 개수만큼
후위순회의 시작점부터 해당 개수만큼 오른쪽으로 이동하여 그 시작점을 정하고 마지막 노드를 제외한 모든 노드들이다.
- 먼저, 후위순회는 부모 노드를 가장 마지막에 탐색하며, 이러한 동작 방식은 트리의 '루트 노드'가 후위순회의 가장 마지막 순서에 오도록 합니다.
- 다음으로, 중위 순회는 '루트 노드'가 가운데에 위치하며, 해당 노드를 기준으로 왼쪽이 '왼쪽 서브 트리', 그리고 오른쪽이 '오른쪽 서브 트리'입니다.
- 결과적으로, 후위순회의 마지막 정점을 찾고, 해당 정점이 중위순회 내 위치한 곳을 기준으로 왼쪽과 오른쪽 서브트리로 분할하여, 재귀적으로 순회하는 것으로 '전위순회'를 가능케 합니다.
- 정리하면, 후위순회의 마지막 노드는 '부모 노드'가 되며, 해당 노드가 중위순회 내 어디에 위치하는지 찾고, 중위 순회 내 해당 위치를 기준으로 왼쪽에 있는 노드들이 '왼쪽 서브 트리', 그리고 오른쪽에 있는 노드들이 '오른쪽 서브 트리'라는 점을 기억하면 된다.
#3. 코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> inorder, postorder, position;
void solve (int in_start, int in_end, int post_start, int post_end) {
if (in_start > in_end || post_start > post_end)
return;
// #1. 후위 순회의 마지막 노드는 '루트 노드'
int root = postorder[post_end];
cout << root << ' ';
// #2. 왼쪽 서브 트리에 대한 재귀
// -> 'in_start ~ root-1' = 중위순회 내 루트 노드 기준 왼쪽 서브트리
// -> 'pos_start ~ pos_start + root-1 - in_start' : 후위순회 내 루트 노드 기준 왼쪽 서브트리
solve(in_start, position[root]-1, post_start, post_start + (position[root]-1 - in_start));
// #3. 오른쪽 서브 트리에 대한 재귀
// -> 'root+1 ~ in_end' = 중위순회 내 루트 노드 기준 오른쪽 서브트리
// -> 'pos_start + root - in_start' = 후위순회 내 루트 노드 기준 오른쪽 서브트리
solve(position[root]+1, in_end, post_start + (position[root] - in_start), post_end-1);
}
int main() {
int n;
cin >> n;
// 중위 순회
inorder.resize(n+1);
// 후위 순회
postorder.resize(n+1);
// 중위 순회에서 각 항목의 위치 값
position.resize(n+1);
// #1.중위 순회 중 본인의 위치를 기억
for (int i=1; i<=n; i++) {
cin >> inorder[i];
position[inorder[i]] = i;
}
// #2. 후위 순회
for (int i=1; i<=n; i++)
cin >> postorder[i];
solve(1, n, 1, n);
return 0;
}
'문제 풀이 > BOJ 문제 풀이' 카테고리의 다른 글
| [BOJ알고리즘, C++]#24479_알고리즘 수업 - 깊이 우선 탐색 1, DFS, 재귀 DFS, 스택 DFS (0) | 2023.12.14 |
|---|---|
| [BOJ알고리즘, C++]#5639_이진 검색 트리, 이진 탐색 트리 순회, 전위순회, 후위순회, 전위순회를 통해 후위순회 구하기 (0) | 2023.12.02 |
| [BOJ알고리즘, C++]#10798_세로 읽기, getline() (1) | 2023.11.23 |
| [BOJ알고리즘, C++]#11286_절댓값 힙, 힙, 최소 힙, 최대 힙, 우선순위 큐, priority_queue (1) | 2023.11.23 |
| [BOJ알고리즘, C++]#10799_쇠 막대기, 선형 자료구조, 스택 (2) | 2023.11.23 |
