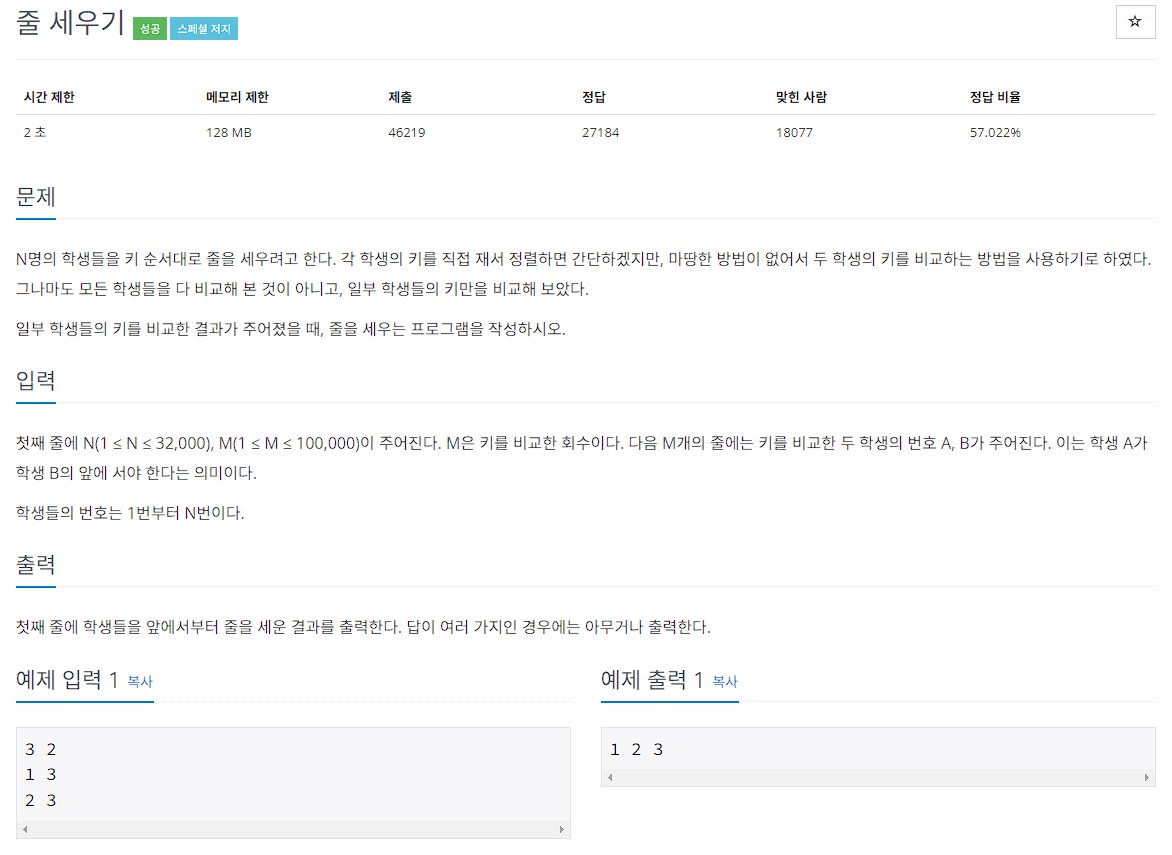
#1. 문제

#2. 풀이
1. 위상 정렬
[자료구조]#6_그래프
#0. 개념 1. 그래프? [정의] : 그래프는 노드와 간선들의 집합으로 이루어진 비 선형 자료구조입니다. 그래프의 노드들은 간선을 통해 연결되어 일종의 네트워크를 형성합니다. 그래프는 노드와
webddevys.tistory.com
Details
위상 정렬은 비순환 유향 그래프(DAG)의 각 정점들의 선행 관계를 유지하며 나열하는 정렬 작업입니다. 그래프 내 순환 구조가 존재할 경우, 두 정점의 순서를 정할 수 없기 때문에 위상 정렬은 오직 비순환 유향 그래프에 적용 가능한 정렬 작업입니다.
2. DFS? BFS?
1. DFS를 활용한 위상 정렬
DFS를 활용한 위상 정렬은 DFS 수행 과정에서 각 정점을 방문할 때마다 stack에 정점을 삽입합니다. 마지막으로, 그 순서를 결정할 때 stack의 가장 위에 위치한 정점부터 차례대로 꺼내며 그 순서를 결정합니다.
2. BFS와 진입 차수를 활용한 위상 정렬
진입 차수와 BFS를 활용한 위상 정렬은 먼저 진입 차수가 0인 정점들을 미리 큐에 삽입합니다. 그리고, BFS를 수행하며 현재 정점의 인접 정점들의 진입 차수 확인하고, 진입 차수가 0일 경우 정렬 목록에 추가하고, 진입 차수가 1 이상일 경우 -1을 차감하고 큐에 삽입합니다.
#3. 코드
1. DFS 위상 정렬
#include <iostream>
#include <vector>
#include <string>
#include <unordered_map>
#include <stack>
using namespace std;
int N, M;
// #1. 재귀 DFS 함수
void DFS(int node, unordered_map<int, vector<int>>& graph, vector<bool>& visited, stack<int>& s)
{
// #1. 방문 여부 체크
visited[node] = true;
// #2. 다음 정점 순회
for(auto& next : graph[node])
{
if(!visited[next])
{
DFS(next, graph, visited, s);
}
}
// #3. 현재 항목을 스택에 삽입
s.push(node);
}
// #2. 재귀 DFS를 활용하는 위상 정렬 함수
void TopologicalSort(unordered_map<int, vector<int>>& graph)
{
// #1. 방문 여부
vector<bool> visited(N+1, false);
// #2. 순서를 담은 스택
stack<int> s;
// #2. 재귀 DFS 수행
for(int i=1; i<=N; ++i)
{
if(!visited[i])
DFS(i, graph, visited, s);
}
// #3. 스택에서 결과 값 출력
while(!s.empty())
{
int cur = s.top();
s.pop();
cout << cur << ' ';
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> N >> M;
// #1. um 형식의 그래프 선언
unordered_map<int, vector<int>> graph;
// #2. 그래프 구성
for(int i=0; i<M; ++i)
{
int node1, node2;
cin >> node1 >> node2;
graph[node1].push_back(node2);
}
// #3. 위상정렬 호출
TopologicalSort(graph);
return 0;
}
2. BFS와 진입차수 위상 정렬
#include <iostream>
#include <vector>
#include <string>
#include <unordered_map>
#include <queue>
using namespace std;
int N, M;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> N >> M;
// #1. um 형식의 그래프
unordered_map<int, vector<int>> graph;
// #2. 진입 차수
vector<int> InDegree(N+1);
// #3. 그래프 구성
for(int i=0; i<M; ++i)
{
int node1, node2;
cin >> node1 >> node2;
// 그래프에 삽입
graph[node1].push_back(node2);
// 진입 차수 갱신
InDegree[node2]++;
}
// #4. queue 선언
queue<int> q;
// #5. 진입 차수가 0인 정점 queue에 삽입
for(int i=1; i<=N; ++i)
{
if(InDegree[i] == 0)
q.push(i);
}
// #6. 큐 순회
while(!q.empty())
{
// 큐의 첫 번째 항목 제거
int cur = q.front();
q.pop();
// 결과 출력
cout << cur << ' ';
// 첫 번째 항목의 인접 정점들 순회
for(auto& neighbor : graph[cur])
{
InDegree[neighbor]--;
if(InDegree[neighbor] == 0)
q.push(neighbor);
}
}
return 0;
}
'문제 풀이 > BOJ 문제 풀이' 카테고리의 다른 글
| [BOJ알고리즘, C++]#1647_도시 분할 계획, MST, 최소 신장 트리, 크루스칼, 프림, 솔린 (1) | 2023.12.21 |
|---|---|
| [BOJ알고리즘, C++]#4386_별자리 만들기, MST, 최소 신장 트리, 크루스칼, 프림, 솔린 (1) | 2023.12.21 |
| [BOJ알고리즘, C++]#1753_최단 경로, 다익스트라 (0) | 2023.12.15 |
| [BOJ알고리즘, C++]#1922_네트워크 연결, MST, 최소 신장 트리, 크루스칼, 프림, 솔린 (0) | 2023.12.15 |
| [BOJ알고리즘, C++]#1197_최소 스패닝 트리, MST, 크루스칼, 프림, 솔린 (0) | 2023.12.15 |
#1. 문제


#2. 풀이
1. 위상 정렬
[자료구조]#6_그래프
#0. 개념 1. 그래프? [정의] : 그래프는 노드와 간선들의 집합으로 이루어진 비 선형 자료구조입니다. 그래프의 노드들은 간선을 통해 연결되어 일종의 네트워크를 형성합니다. 그래프는 노드와
webddevys.tistory.com
Details
위상 정렬은 비순환 유향 그래프(DAG)의 각 정점들의 선행 관계를 유지하며 나열하는 정렬 작업입니다. 그래프 내 순환 구조가 존재할 경우, 두 정점의 순서를 정할 수 없기 때문에 위상 정렬은 오직 비순환 유향 그래프에 적용 가능한 정렬 작업입니다.
2. DFS? BFS?
1. DFS를 활용한 위상 정렬
DFS를 활용한 위상 정렬은 DFS 수행 과정에서 각 정점을 방문할 때마다 stack에 정점을 삽입합니다. 마지막으로, 그 순서를 결정할 때 stack의 가장 위에 위치한 정점부터 차례대로 꺼내며 그 순서를 결정합니다.
2. BFS와 진입 차수를 활용한 위상 정렬
진입 차수와 BFS를 활용한 위상 정렬은 먼저 진입 차수가 0인 정점들을 미리 큐에 삽입합니다. 그리고, BFS를 수행하며 현재 정점의 인접 정점들의 진입 차수 확인하고, 진입 차수가 0일 경우 정렬 목록에 추가하고, 진입 차수가 1 이상일 경우 -1을 차감하고 큐에 삽입합니다.
#3. 코드
1. DFS 위상 정렬
#include <iostream>
#include <vector>
#include <string>
#include <unordered_map>
#include <stack>
using namespace std;
int N, M;
// #1. 재귀 DFS 함수
void DFS(int node, unordered_map<int, vector<int>>& graph, vector<bool>& visited, stack<int>& s)
{
// #1. 방문 여부 체크
visited[node] = true;
// #2. 다음 정점 순회
for(auto& next : graph[node])
{
if(!visited[next])
{
DFS(next, graph, visited, s);
}
}
// #3. 현재 항목을 스택에 삽입
s.push(node);
}
// #2. 재귀 DFS를 활용하는 위상 정렬 함수
void TopologicalSort(unordered_map<int, vector<int>>& graph)
{
// #1. 방문 여부
vector<bool> visited(N+1, false);
// #2. 순서를 담은 스택
stack<int> s;
// #2. 재귀 DFS 수행
for(int i=1; i<=N; ++i)
{
if(!visited[i])
DFS(i, graph, visited, s);
}
// #3. 스택에서 결과 값 출력
while(!s.empty())
{
int cur = s.top();
s.pop();
cout << cur << ' ';
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> N >> M;
// #1. um 형식의 그래프 선언
unordered_map<int, vector<int>> graph;
// #2. 그래프 구성
for(int i=0; i<M; ++i)
{
int node1, node2;
cin >> node1 >> node2;
graph[node1].push_back(node2);
}
// #3. 위상정렬 호출
TopologicalSort(graph);
return 0;
}
2. BFS와 진입차수 위상 정렬
#include <iostream>
#include <vector>
#include <string>
#include <unordered_map>
#include <queue>
using namespace std;
int N, M;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> N >> M;
// #1. um 형식의 그래프
unordered_map<int, vector<int>> graph;
// #2. 진입 차수
vector<int> InDegree(N+1);
// #3. 그래프 구성
for(int i=0; i<M; ++i)
{
int node1, node2;
cin >> node1 >> node2;
// 그래프에 삽입
graph[node1].push_back(node2);
// 진입 차수 갱신
InDegree[node2]++;
}
// #4. queue 선언
queue<int> q;
// #5. 진입 차수가 0인 정점 queue에 삽입
for(int i=1; i<=N; ++i)
{
if(InDegree[i] == 0)
q.push(i);
}
// #6. 큐 순회
while(!q.empty())
{
// 큐의 첫 번째 항목 제거
int cur = q.front();
q.pop();
// 결과 출력
cout << cur << ' ';
// 첫 번째 항목의 인접 정점들 순회
for(auto& neighbor : graph[cur])
{
InDegree[neighbor]--;
if(InDegree[neighbor] == 0)
q.push(neighbor);
}
}
return 0;
}
'문제 풀이 > BOJ 문제 풀이' 카테고리의 다른 글
| [BOJ알고리즘, C++]#1647_도시 분할 계획, MST, 최소 신장 트리, 크루스칼, 프림, 솔린 (1) | 2023.12.21 |
|---|---|
| [BOJ알고리즘, C++]#4386_별자리 만들기, MST, 최소 신장 트리, 크루스칼, 프림, 솔린 (1) | 2023.12.21 |
| [BOJ알고리즘, C++]#1753_최단 경로, 다익스트라 (0) | 2023.12.15 |
| [BOJ알고리즘, C++]#1922_네트워크 연결, MST, 최소 신장 트리, 크루스칼, 프림, 솔린 (0) | 2023.12.15 |
| [BOJ알고리즘, C++]#1197_최소 스패닝 트리, MST, 크루스칼, 프림, 솔린 (0) | 2023.12.15 |
