[확률과 통계]#3_이항 정리, 파스칼 삼각형
확률과 통계 과목의 "이항 정리"와 "파스칼 삼각형"에 대해 공부합니다.
Overview
- 이항 정리
- 파스칼의 삼각형
#0. 이항 정리
1. 이항 정리?
- 이항 정리(Binomial Theorem)는 이항식의 거듭제곱을 이항 계수를 계수로 하는 일련의 단항식들의 합으로 전개하는 정리입니다.
2. 다항식
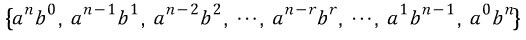
- 이항정리에서 소개되는 (a+b)ⁿ는 n차 다항식으로, 전개하면 위와 같은 형태로 나타납니다.

- 다항식 (a+b) ³을 전개해 보겠습니다.
- 이때, 단항식의 계수들을 정리하면, 1, 3, 3, 1이 나옵니다.
- 우리는 간단한 방법을 통해 다항식을 통해 전개하여 나오는 계수들을 찾아낼 수 있습니다.
3. 이항 계수와 조합의 관계
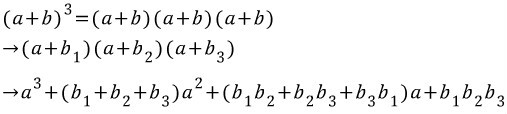
- 가장 먼저, (a+b)³를 (a₁+b₁) x (a₂ + b₂) x (a₃ + b₃)로 풀어 생각해 보겠습니다. 물론, a₁ = a₂ = a₃이며, 마찬가지로 b₁ = b₂ = b₃입니다. 이렇게 생각해 보겠습니다. 빨간 공 3개 그리고 파란 공 3개에서 빨간색을 a로 가정하고, b를 파란색으로 가정해 보겠습니다. 3개의 파란색 공은 서로 다른 객체일 뿐 속성이 다르지 않죠? b₁, b₂, 그리고 b₃를 각각 같은 b 속성의 3개의 다른 개체들로 취급하여 진행해보겠습니다. 편의를 위해 a를 세는 것은 생략하고 b에 집중해 보죠.
- 두 번째 단항식을 살펴보면, ( b₁ + b₂ + b₃ ) x a²는 곧 a² b₁ + a²b₂ + a² b₃를 의미합니다. 그리고, (a) 빨간색 공을 두 개 뽑고 (b₁) 파란색 첫 번째 공, (b₂) 파란색 두 번째 공, 그리고 (b₃) 파란색 세 번째 공 중 한 개를 뽑을 확률들과 같은 의미입니다.
- 이어서, 세 개의 빨간색 공과 세 개의 파란색 공 중 빨간색 공을 두 개 뽑고 나머지 한 개는 파란색 공을 뽑을 확률은 "조합"에서 ₃C₂ 혹은 ₃C₁ 같은 의미입니다. 왜냐하면, 서로 다른 두 개의 속성 중 한 속성에 기준을 두어 세 개의 공 중 빨간색이 두 개가 뽑힐 확률은 ₃C₂이며, 이는 곧 세 개의 공중 파란색이 한 개만 뽑힐 확률 ₃C₁과 같기 때문입니다. 아시다시피, nCr = nCn-r 이기 때문입니다.
3. 이항 정리

- 결과적으로, (a+b)ⁿ의 이항 계수는 곧 nCr입니다.
#2. 파스칼의 삼각형
1. 개념

- 먼저, 위에서 살펴본 다항식 (a+b)ⁿ를 n=1일 경우부터 시작해 차례대로 전개해 보겠습니다.
- 위 그림을 살펴보면, 차례대로 전개된 다항식의 계수들에서 규칙이 발생하는 것을 알 수 있습니다.
- 더 자세히 알아보기 위해 위 전개식들의 계수들만 "삼각형"으로 재 배치 해보겠습니다.
2. 파스칼의 삼각형

- 첫 번째 그림은 이항 계수들을 삼각형으로 배치한 그림이며, 두 번째 그림은 계수들을 삼각형으로 배치한 그림입니다.
- 위에서 살펴본 내용에 따르면 (a + b)ⁿ의 이항 계수는 곧 nCr이며, 조합의 성질을 통해 위 삼각형 그림에서 규칙들을 손쉽게 찾아낼 수 있습니다.
3. 파스칼의 삼각형과 조합의 성질
- 첫 번재 성질은 nC₁ 과 nCn은 1이며, 곧 삼각형의 양 끝에 있는 값들은 모두 1입니다.
- 두 번째 성질은 n-₁Cr-₁ + n-₁Cr = nCr이며, 임의의 줄에 연속해서 위치하는 두 개의 값을 더하면 두 값의 다음 줄 가운데에 위치한 값과 같습니다.
- 세 번째 성질은 nCr = nCn-r이며, 삼각형은 좌우 대칭이기 때문입니다.
- 네 번째 성질은 대각선 상에 위치한 값들을 모두 더하면 마지막 값의 반대 대각선 상에 위치한 값이 됩니다.
'수학 > 확률과 통계' 카테고리의 다른 글
| [확률과 통계]#2 조합, nCr (0) | 2022.12.11 |
|---|---|
| [확률과 통계]#1 순열, nPr (2) | 2022.12.10 |
[확률과 통계]#3_이항 정리, 파스칼 삼각형
확률과 통계 과목의 "이항 정리"와 "파스칼 삼각형"에 대해 공부합니다.
Overview
- 이항 정리
- 파스칼의 삼각형
#0. 이항 정리
1. 이항 정리?
- 이항 정리(Binomial Theorem)는 이항식의 거듭제곱을 이항 계수를 계수로 하는 일련의 단항식들의 합으로 전개하는 정리입니다.
2. 다항식
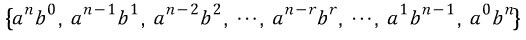
- 이항정리에서 소개되는 (a+b)ⁿ는 n차 다항식으로, 전개하면 위와 같은 형태로 나타납니다.

- 다항식 (a+b) ³을 전개해 보겠습니다.
- 이때, 단항식의 계수들을 정리하면, 1, 3, 3, 1이 나옵니다.
- 우리는 간단한 방법을 통해 다항식을 통해 전개하여 나오는 계수들을 찾아낼 수 있습니다.
3. 이항 계수와 조합의 관계
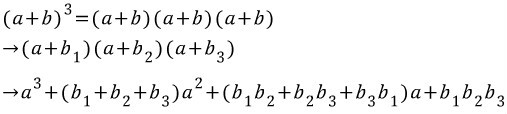
- 가장 먼저, (a+b)³를 (a₁+b₁) x (a₂ + b₂) x (a₃ + b₃)로 풀어 생각해 보겠습니다. 물론, a₁ = a₂ = a₃이며, 마찬가지로 b₁ = b₂ = b₃입니다. 이렇게 생각해 보겠습니다. 빨간 공 3개 그리고 파란 공 3개에서 빨간색을 a로 가정하고, b를 파란색으로 가정해 보겠습니다. 3개의 파란색 공은 서로 다른 객체일 뿐 속성이 다르지 않죠? b₁, b₂, 그리고 b₃를 각각 같은 b 속성의 3개의 다른 개체들로 취급하여 진행해보겠습니다. 편의를 위해 a를 세는 것은 생략하고 b에 집중해 보죠.
- 두 번째 단항식을 살펴보면, ( b₁ + b₂ + b₃ ) x a²는 곧 a² b₁ + a²b₂ + a² b₃를 의미합니다. 그리고, (a) 빨간색 공을 두 개 뽑고 (b₁) 파란색 첫 번째 공, (b₂) 파란색 두 번째 공, 그리고 (b₃) 파란색 세 번째 공 중 한 개를 뽑을 확률들과 같은 의미입니다.
- 이어서, 세 개의 빨간색 공과 세 개의 파란색 공 중 빨간색 공을 두 개 뽑고 나머지 한 개는 파란색 공을 뽑을 확률은 "조합"에서 ₃C₂ 혹은 ₃C₁ 같은 의미입니다. 왜냐하면, 서로 다른 두 개의 속성 중 한 속성에 기준을 두어 세 개의 공 중 빨간색이 두 개가 뽑힐 확률은 ₃C₂이며, 이는 곧 세 개의 공중 파란색이 한 개만 뽑힐 확률 ₃C₁과 같기 때문입니다. 아시다시피, nCr = nCn-r 이기 때문입니다.
3. 이항 정리

- 결과적으로, (a+b)ⁿ의 이항 계수는 곧 nCr입니다.
#2. 파스칼의 삼각형
1. 개념

- 먼저, 위에서 살펴본 다항식 (a+b)ⁿ를 n=1일 경우부터 시작해 차례대로 전개해 보겠습니다.
- 위 그림을 살펴보면, 차례대로 전개된 다항식의 계수들에서 규칙이 발생하는 것을 알 수 있습니다.
- 더 자세히 알아보기 위해 위 전개식들의 계수들만 "삼각형"으로 재 배치 해보겠습니다.
2. 파스칼의 삼각형

- 첫 번째 그림은 이항 계수들을 삼각형으로 배치한 그림이며, 두 번째 그림은 계수들을 삼각형으로 배치한 그림입니다.
- 위에서 살펴본 내용에 따르면 (a + b)ⁿ의 이항 계수는 곧 nCr이며, 조합의 성질을 통해 위 삼각형 그림에서 규칙들을 손쉽게 찾아낼 수 있습니다.
3. 파스칼의 삼각형과 조합의 성질
- 첫 번재 성질은 nC₁ 과 nCn은 1이며, 곧 삼각형의 양 끝에 있는 값들은 모두 1입니다.
- 두 번째 성질은 n-₁Cr-₁ + n-₁Cr = nCr이며, 임의의 줄에 연속해서 위치하는 두 개의 값을 더하면 두 값의 다음 줄 가운데에 위치한 값과 같습니다.
- 세 번째 성질은 nCr = nCn-r이며, 삼각형은 좌우 대칭이기 때문입니다.
- 네 번째 성질은 대각선 상에 위치한 값들을 모두 더하면 마지막 값의 반대 대각선 상에 위치한 값이 됩니다.
'수학 > 확률과 통계' 카테고리의 다른 글
| [확률과 통계]#2 조합, nCr (0) | 2022.12.11 |
|---|---|
| [확률과 통계]#1 순열, nPr (2) | 2022.12.10 |
