[확률과 통계]#1 순열, nPr

 

[확률과 통계]#1 순열과 조합

 

확률과 통계 과목의 "순열과 조합"에 대해 공부합니다.

 

---

 

Overview

 

1. 순열과 조합의 의미
2. 팩토리얼
3. 원순열
4. 중복 순열
5. 같은 것이 있는 순열

 

순열과 조합

1. 순열?

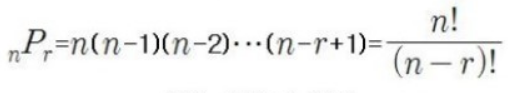
Details

 

• 서로 다른 N개의 항목들 중에서 R개를 선택해 일렬로 나열한 것. nPr(Permutation)로 표현합니다.
• 조합(nCr)과 순열의 차이점은 "선택"만 할 것인가? 아니라면, "선택 후 나열"까지 고려할 것인가?입니다.

 

2. 성질

 

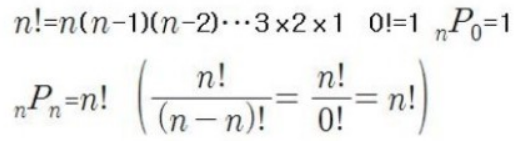
Details

 

• 순열의 몇 가지 특징들을 살펴보겠습니다.
• 먼저, nPr에서 "r" 값이 0일 때, nPr은 무조건 1이 됩니다. 당연하죠?
• 더불어, n 개 중 n개 모두 뽑을 경우 nPn은 간단히 "n!"인 것을 알 수 있습니다!

 

예제

 

문제) 숫자 카드 1, 2, 3, 4 네 개의 카드들 중에서 3장의 카드를 뽑아서 3자리 자연수를 만드는 경우의 수?

 

• 답) 4 * 3 * 2 = 24
• 전형적인 "순열"을 활용하여 풀이하는 문제입니다. nPr로 풀이할 수 있으며, 여기서 "n = 4", 그리고 "r = 3"가 됩니다.

 

 

원순열

1. 원순열?

 

Details

 

• 우리가 알고 있는 "일렬로 세우는" 순열의 형태에서, 서로 다른 N개의 원소를 원형으로 배열하는 것을 원순 열이라 합니다.

 

2. 원순열을  푸는 두 가지 방법

 

• 원순열을 풀기 위한 두 가지 방법 중 "직순열 / 중복의 수" 방법을 알아보겠습니다! 
• 개요는 이러합니다. 먼저, 직순열로 계산한 경우의 수를 "중복이 생기는 경우의 수"로 나누는 것입니다.

 

예제

 

 

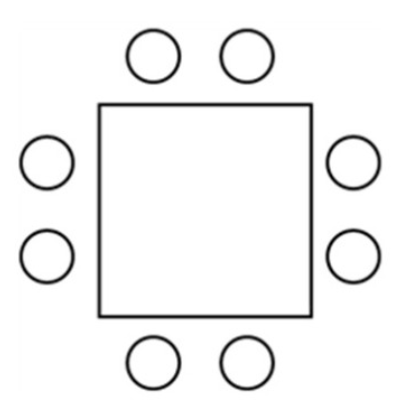
문제) 위 그림과 같은 정사각형 모양의 탁자에 8명이 둘러앉는 방법의 수는? (단, 회전하여 일치하는 경우는 같은 경우)

 

 

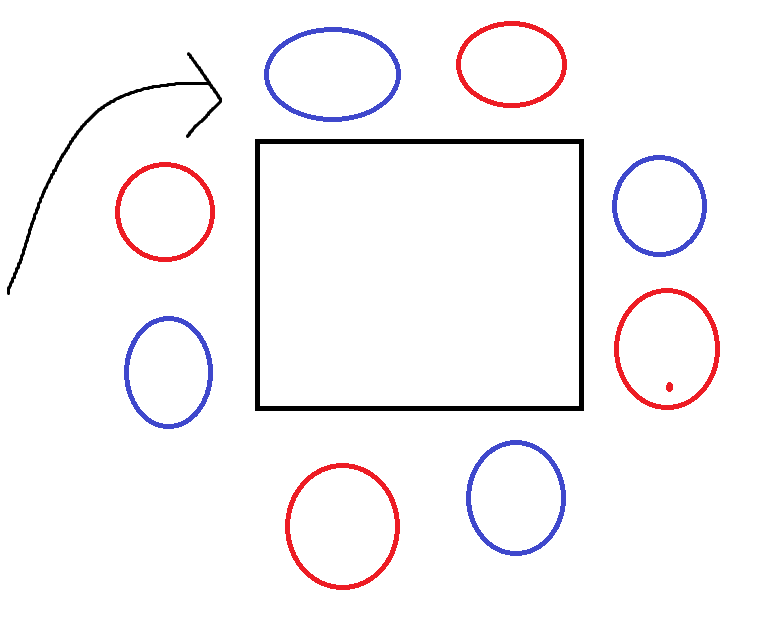
• 간단합니다. 먼저 직순열(nPr)로 경우의 수를 계산합니다. "n=8"이고 "r=8" 이니까, 8! 이 나옵니다.
• 다음으로 중복되는 경우의 수를 고려해야합니다.
• 정사각형의 각 변에 앉을 수 있는 자리는 2개씩이며, 먼저 정사각형을 시계 방향으로 한 번씩 회전해봅니다.
• 빨간색 원으로 표시된 자리 혹은 파란색 원으로 표시된 자리는 회전할 때마다 중복이 발생합니다!
• 즉, 왼쪽 변의 빨간색 원 자리에 앉은 사람은 윗 변의 빨간색 원 자리에 앉은 것과 다름이 없다는 것이죠. 
• 총 4가지 중복되는 경우의 수가 발생합니다!
• 답) 8! / 4

 

 

중복 순열

1. 중복 순열?

 

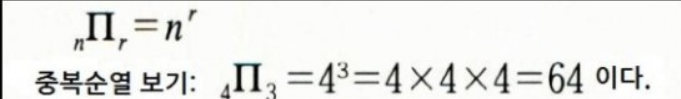
Details

 

• 중복순열이란 서로 다른 n가지 대상에서 중복을 허용하여 r개를 선택하여 순서 있게 배열하는 것입니다.
• n개의 원소를 중복 없이 r개 선택하는 순열의 경우 "nPr"로 표기했지만, 중복을 혀용 할 경우 "n∏r" 표기합니다.

 

예제

 

문제) 서로 다른 편지 3통을 서로 다른 2개의 우체통에 넣는 방법의 수를 구하여라. (단, 편지를 넣지 않는 우체통 있음)

 

• 답 : 2∏3 = 2 * 2 * 2 = 8가지 방법

 

문제) 5명의 여행자가 3곳의 호텔에 투숙하는 방법의 수를 구하여라(단, 투숙하지 않는 호텔도 있음)

 

• 답) 3∏5 = 3 * 3 * 3 * 3 * 3 = 243가지 방법

 

같은 것이 있는 순열 

1. 같은 것이 있는 순열?

 

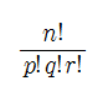
• 같은 것이 있는 순열이란, 우리가 고려해야 할 원소들이 각각 서로 다른 원소가 아니라, 몇몇 원소들은 서로를 구별할 수 없는, 즉 동일한 속성을 갖는 원소들을 주어진 조건 하에 선택하고 나열하는 것을 의미합니다. 사소한 차이지만, 결과는 사소하지 않죠!

 

예제

 

문제) 1번 카드가 3장, 2번 카드가 1장, 그리고 3번 카드가 1장 있을 때, 5자리의 수를 만드는 방법의 수를 구하여라

 

• 1번 카드가 총 3장이 있습니다. 이 3장의 카드들은 서로의 위치가 바뀌어도 결과에 영향을 미치지 않습니다!
• 따라서, nPr(순열) 공식을 통해 계산한 5! 는 정답이 아닙니다!
• 1번 카드들끼리 위치가 바뀌는 "중복되는 경우의 수"를 고려해야죠!
• 앞서, 원순열 문제를 푸는 방법 중 직순열을 통해 계산한 경우의 수를 중복되는 경우의 수로 나누어주었죠?
• 맞습니다! 중복되는 경우의 수를 찾아 5! 에 나누어주면 됩니다.
• 1번 카드들끼리 위치가 바뀌는 경우의 수는 총 3!입니다! 
• 답) 5! / 3!

 

 

Summary