문제 풀이/BOJ 문제 풀이
[BOJ알고리즘, C++]#5639_이진 검색 트리, 이진 탐색 트리 순회, 전위순회, 후위순회, 전위순회를 통해 후위순회 구하기
Hardii2
2023. 12. 2. 15:40
[BOJ알고리즘, C++]#5639_이진 검색 트리
BOJ 알고리즘 문제 풀이, 5639번 문제 "이진 검색 트리"
이진 탐색 트리의 전위순회 결과를 통해 후위순회 결과를 구하는 방법
Overview
- 문제
- 풀이
- 코드
#1. 문제
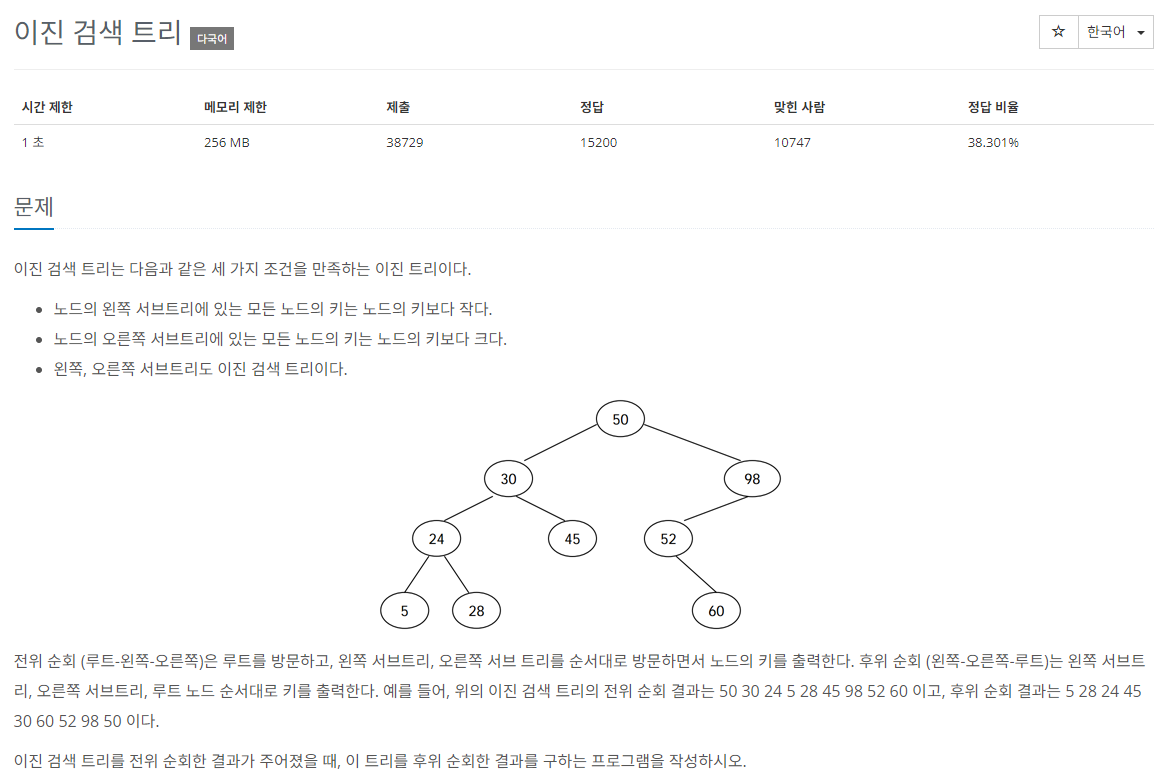
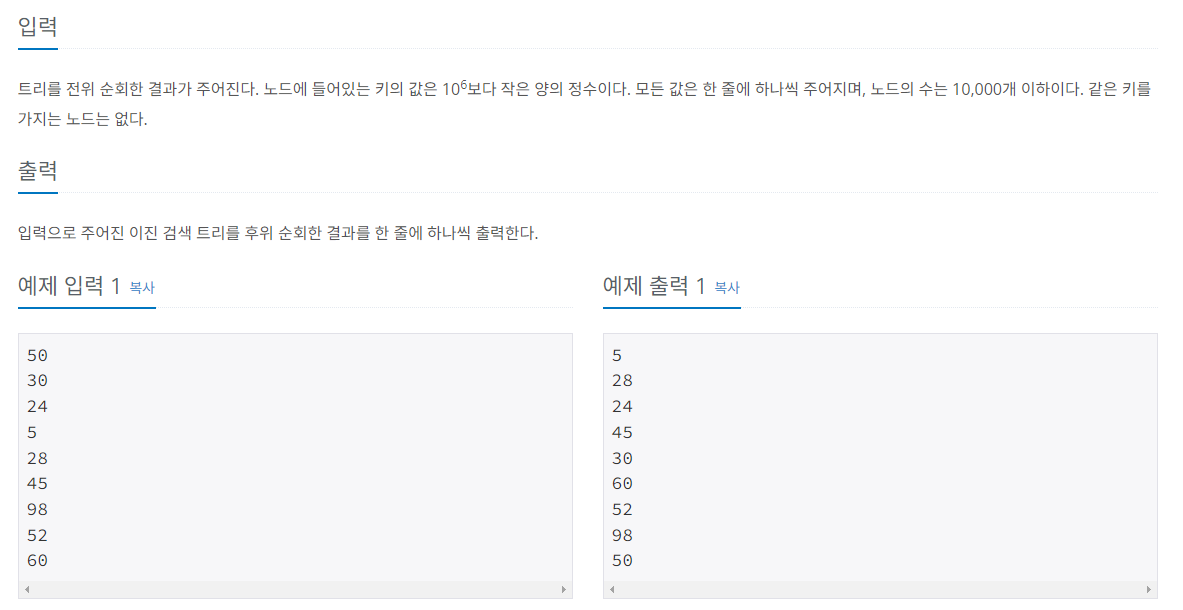
#2. 풀이
1. 트리
[자료구조]#5_트리
[자료구조]#5_트리 트리 자료구조에 대해 알아보겠습니다. Overview 개념 이진트리 순회 이진 탐색 트리 균형 이진트리 AVL 트리 레드-블랙 트리 Map, Set 힙 #0. 개념 1. 트리? [정의] : 트리는 1:n 관계의
webddevys.tistory.com
- [정의] : 트리는 1:n 관계의 계층 구조를 갖는 비 선형 자료구조입니다. 트리는 노드와 노드 간 연결관계를 표현하는 간선으로 이루어져 있습니다.
- [특징] : 트리의 두 가지 주요 특징은 계층 구조와 비순환 구조입니다. 트리의 노드는 부모-자식 관계 갖고 계층구조를 형성하며, 순환 구조를 갖지 않습니다.
2. 이진 탐색 트리
- [정의] : 이진 탐색 트리는 이진트리의 한 종류로, 부모-자식의 계층 관계에서 왼쪽 자식 노드의 값은 부모 노드의 값보다 작거나 같고, 오른쪽 자식 노드의 값은 부모 노드의 값보다 크거나 같은 형태를 유지합니다.
- [특징]
- 이진 탐색 트리의 모든 노드는 값을 가지며, 최대 두 개의 자식 노드를 갖습니다.
- 이진 탐색 트리의 왼쪽 자식 노드의 값은 부모 노드의 값보다 작거나 같고, 오른쪽 자식 노드의 값은 부모 노드의 값보다 크거나 같습니다.
- 이진 탐색 트리의 모든 서브 트리는 또한 이진 탐색 트리입니다.
3. 트리의 순회
- [개념] : 트리의 순회는 모든 노드를 탐색 할 때, 세 가지 방문 순서에 기반합니다.
- [종류]
- 전위순회(Preorder) : 부모 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드
- 중위순회(Inorder) : 왼쪽 자식 노드 -> 부모 노드 -> 오른쪽 자식 노드
- 후위순회(Postorder) : 왼쪽 자식 노드 -> 오른쪽 노드 -> 부모 노드
3. 이진 탐색 트리의 전위순회
전위 순회 = '50 30 24 5 28 45 98 52 60'
1. 왼쪽 서브트리 = '50 [30 24 5 28 45] 98 52 60'
2. 오른쪽 서브트리 = '50 30 24 5 28 45 [98 52 60]'
3. root = 전위순회[pre_start]
4. 오른쪽 서브트리 = root 노드 보다 큰 수의 위치 ~ pre_end
5. 왼쪽 서브트리 = pre_start+1 ~ root 노드 보다 큰 수의 위치-1
6. 위 과정을 재귀적으로 수행
- 먼저, 전위순회의 첫 번째 노드는 트리의 '루트 노드'입니다.
- 다음으로, 두 번째 노드가 왼쪽 자식 노드입니다.
- 마지막으로, 가장 첫 번째로 만나는 루트 노드보다 큰 값을 가진 노드가 오른쪽 자식 노드입니다.
- 위 규칙을 기반으로, 전위순회 내 루트 노드와 왼쪽 서브트리와 오른쪽 서브트리를 분할하고, 이 과정을 재귀적으로 수행합니다.
#3. 코드
#include <iostream>
#include <vector>
#include <string>
using namespace std;
vector<int> tree;
int num;
void findPostorder(int pre_start, int pre_end)
{
if(pre_start > pre_end)
return;
// #1. 루트 노드 찾기, 전위순회의 첫 번째 순서
int root = tree[pre_start];
// #2. 루트 노드 다음으로 큰 수가 오른쪽 자식 노드가 된다.
int rightChildIdx = pre_start+1;
while(rightChildIdx <= pre_end && tree[rightChildIdx] <= root)
{
rightChildIdx++;
}
// #3. 왼쪽 서브트리에 대해 재귀함수 호출
findPostorder(pre_start+1, rightChildIdx-1);
// #4. 오른쪽 서브트리에 대해 재귀함수 호출
findPostorder(rightChildIdx, pre_end);
// #5. 루트 노드 출력
cout << root << '\n';
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
while(cin >> num)
{
tree.push_back(num);
}
findPostorder(0, tree.size()-1);
return 0;
}