문제 풀이/BOJ 문제 풀이
[BOJ알고리즘, C++]#1167_트리의 지름, 유 방향 비 순환 가중치 그래프
Hardii2
2023. 7. 28. 21:52
[BOJ알고리즘, C++]#1167_트리의 지름
BOJ 알고리즘 문제 풀이, 1167번 문제 트리의 지름
유 방향 비 순환 가중치 그래프(방향성을 갖는 트리)의 지름을 구하는 방법에 대해 알아보겠습니다.
Overview
- 문제
- 풀이
- 코드
#0. 문제
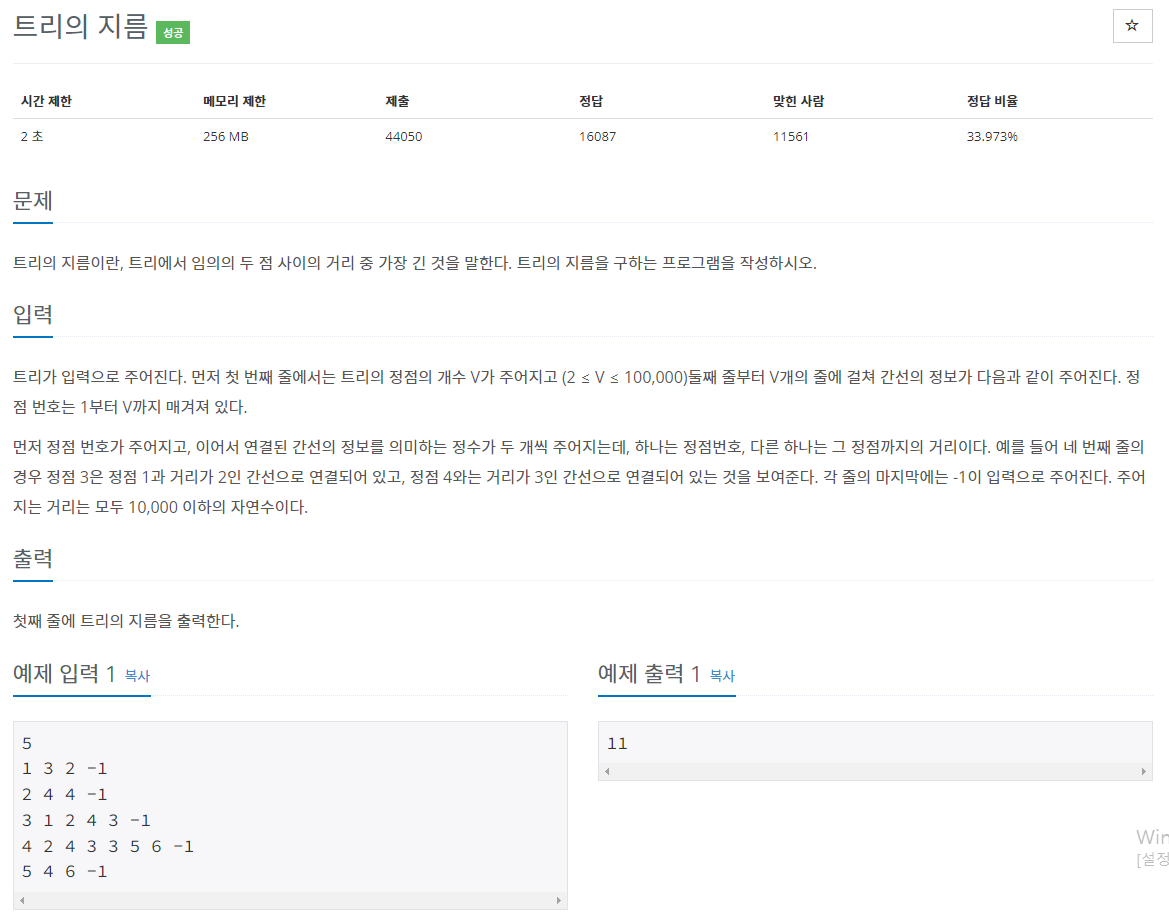
1. 문제
#1. 풀이
1. 트리 자료구조
[자료구조]#5_트리
[자료구조]#5_트리 트리 자료구조에 대해 알아보겠습니다. Overview 개념 이진트리 순회 이진 탐색 트리 균형 이진트리 AVL 트리 레드-블랙 트리 Map, Set 힙 #0. 개념 1. 트리? 트리는 1:n 관계의 계층 구
webddevys.tistory.com
- 트리 자료구조는 1:N 관계를 갖는 비 선형 연결 자료구조입니다.
- 트리는 노드 간 계층 구조를 가지며, 노드 간 연결 관계를 간선으로 표현합니다.
2. 그래프 자료구조
[자료구조]#6_그래프
ㅌ[자료구조]#6_그래프 그래프 자료구조에 대해 알아보겠습니다. Overview 개념 구현 탐색 정렬 신장 트리(Spanning Tree) 최소 신장 트리(Minimum Spanning Tree) #0. 개념 1. 그래프? 그래프는 노드와 간선들의
webddevys.tistory.com
- 그래프 자료구조는 노드와 간선들의 집합으로 이루어진 비 선형 연결 자료구조입니다.
- 그래프는 노드 간 연결 관계를 간선으로 표현하며, 일종의 네트워크를 형성합니다. 그래프는 노드의 개수, 간선의 방향성 유무에 따라서 다양한 형태로 나타납니다.
- 문제는 "트리의 지름"이라고 표현했지만, 방향성을 갖는(Self-Loop이 없는)간선이라고 표현한 것을 보면 유 방향 간선을 갖는 트리이며, 동시에 유 방향 비 순환 가중치 그래프로도 볼 수 있겠습니다. 정리하면, 트리의 간선에 가중치와 방향성을 부여한다면, 해당 트리는 유 방향 비 순환 가중치 그래프의 특별한 형태로 볼 수 있습니다.
3. 트리의 지름
- 트리의 지름을 찾는 방법은 두 번의 DFS(깊이 우선 탐색)입니다.
- 트리의 지름을 찾는 과정의 첫 번째 단계는 DFS(깊이 우선 탐색)을 통해 임의의 시작 정점으로부터 가장 먼 정점을 찾습니다. 이때, 가장 멀 다는 것은 두 정점 사이의 간선들이 갖는 가중치의 합이 최대가 된다는 것을 의미합니다.
- 트리의 지름을 찾는 과정의 두 번째 단계는 DFS(깊이 우선 탐색)을 통해 위에서 얻은 가장 먼 정점을 시작 노드로 설정해 다시 해당 노드로부터 가장 먼 정점을 찾습니다.
- 첫 번째 단계에서 찾은 가장 먼 정점으로부터 두 번째 단계에서 찾은 가장 먼 정점 사이에 존재하는 간선들의 가중치 총 합이 트리의 지름이 됩니다.
- 다만, 주의할점은 문제에서 주어진 트리는 그 간선이 방향성을 가지기 때문에, Parent -> Child 간선이 Child -> Parent 간선으로 취급되어선 안됩니다.
#2. 코드
1. BOJ_1167번 문제
#include <iostream>
#include <vector>
using namespace std;
#define MAX_SIZE 10001
struct Edge
{
int to, weight;
Edge(int _to, int _weight) : to(_to), weight(_weight) {}
};
vector<vector<Edge>> Tree(MAX_SIZE);
vector<bool> visited(MAX_SIZE, false);
int MaxDist, FarthestNode;
void DFS(int cur, int dist, vector<bool>& visited)
{
visited[cur] = true;
if(dist > MaxDist)
{
MaxDist = dist;
FarthestNode = cur;
}
for(auto& edge : Tree[cur])
{
int to = edge.to;
int weight = edge.weight;
if(!visited[to])
{
DFS(to, dist+weight, visited);
}
}
}
int main()
{
ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int n;
cin >> n;
for(int i=0; i<n-1; i++)
{
int parent, child, weight;
cin >> parent >> child >> weight;
Tree[parent].push_back(Edge(child, weight));
Tree[child].push_back(Edge(parent, weight));
}
DFS(1, 0, visited);
MaxDist = 0;
visited.clear();
visited.resize(MAX_SIZE, false);
DFS(FarthestNode, 0, visited);
cout << MaxDist;
return 0;
}