문제 풀이/BOJ 문제 풀이
[BOJ알고리즘, C++]#1991_트리 순회, 전위 순회, 중위 순회, 후위 순회
Hardii2
2023. 7. 28. 21:32
[BOJ알고리즘, C++]#1991_트리 순회
BOJ 알고리즘 문제 풀이, 1991번 문제 트리 순회
트리의 순회 방법에 대해 알아보겠습니다.
Overview
- 문제
- 풀이
- 코드
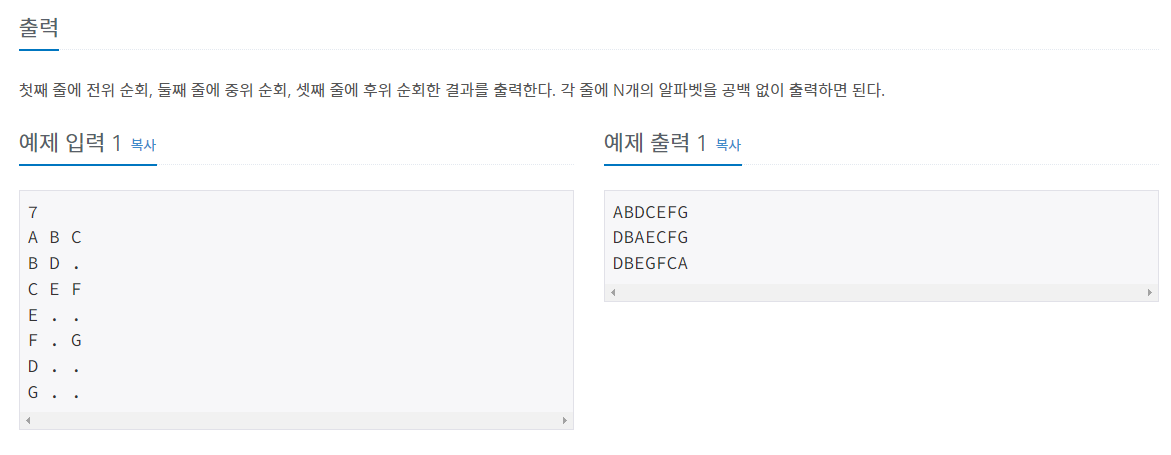
#0. 문제
1. 문제

#1. 풀이
1. 트리 자료구조
[자료구조]#5_트리
[자료구조]#5_트리 트리 자료구조에 대해 알아보겠습니다. Overview 개념 이진트리 순회 이진 탐색 트리 균형 이진트리 AVL 트리 레드-블랙 트리 Map, Set 힙 #0. 개념 1. 트리? 트리는 1:n 관계의 계층 구
webddevys.tistory.com
- 트리 자료구조는 1:N 관계의 비 선형 연결 자료구조입니다. 트리는 노드와 간선으로 구성되며, 각 노드의 연결 관계는 간선으로 표현합니다.
2. 트리 순회
struct Node {
int data;
Node* left;
Node* right;
};
void preorder(Node* root) {
if (root == nullptr) {
return;
}
cout << root->data << " "; // 현재 노드 값 출력
preorder(root->left); // 왼쪽 서브 트리 순회
preorder(root->right); // 오른쪽 서브 트리 순회
}
void inorderTraversal(Node* root) {
if (root == nullptr) {
return;
}
inorderTraversal(root->left); // 왼쪽 서브 트리 순회
cout << root->data << " "; // 현재 노드 값 출력
inorderTraversal(root->right); // 오른쪽 서브 트리 순회
}
void postorderTraversal(Node* root) {
if (root == nullptr) {
return;
}
postorderTraversal(root->left); // 왼쪽 서브 트리 순회
postorderTraversal(root->right); // 오른쪽 서브 트리 순회
cout << root->data << " "; // 현재 노드 값 출력
}
Details
- 전위 순회 : 전위 순회는 트리를 순회하는 방법 중 하나입니다. 트리의 전위 순회는 루트 노드, 왼쪽 서브 트리, 그리고 오른쪽 서브 트리 순서로 순회하는 방법입니다.
- 중위 순회 : 중위 순회는 트리를 순회하는 방법 중 하나입니다. 트리의 전위 순회는 왼쪽 서브 트리, 루트 노드, 그리고 오른쪽 서브 트리 순서로 순회하는 방법입니다.
- 후위 순회 : 후위 순회는 트리를 순회하는 방법 중 하나입니다. 트리의 후위 순회는 왼쪽 서브 트리, 오른쪽 서브 트리, 그리고 루트 노드 순서로 순회하는 방법입니다.
#2. 코드
1. 코드
/*
* [1번 답안] : 배열로 구현한 트리를 활용
* [2번 답안] : 구조체 및 연결 리스트를 활용
*/
// #1. 배열을 활용해 구현한 트리를 활용
#include <iostream>
#include <vector>
using namespace std;
// #1. 전위 순회(루트 -> 왼쪽 -> 오른쪽)
void PreOrder(vector<char>& v, int Idx)
{
if(v[Idx] == '.')
return;
cout << v[Idx];
PreOrder(v, Idx*2);
PreOrder(v, Idx*2+1);
}
// #2. 중위 순회(왼쪽 -> 루트 -> 오른쪽)
void InOrder(vector<char>& v, int Idx)
{
if(v[Idx] == '.')
return;
InOrder(v, Idx*2);
cout << v[Idx];
InOrder(v, Idx*2+1);
}
// #3. 후위 순회(왼쪽 -> 오른쪽 -> 루트)
void PostOrder(vector<char>& v, int Idx)
{
if(v[Idx] == '.')
return;
PostOrder(v, Idx*2);
PostOrder(v, Idx*2+1);
cout << v[Idx];
}
int main()
{
ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int N;
cin >> N;
vector<char> v(26*2+1, '.');
for(int i=0; i<N; i++)
{
char Parent;
char LeftChild;
char RightChild;
cin >> Parent >> LeftChild >> RightChild;
int Idx = Parent - 'A';
v[Idx] = Parent;
if(LeftChild != '.')
v[2*Idx] = LeftChild;
if(RightChild != '.')
v[2*Idx+1] = RightChild;
}
// #1. 전위 순회(루트 -> 왼쪽 -> 오른쪽)
PreOrder(v, 0);
cout << '\n';
// #2. 중위 순회(왼쪽 -> 루트 -> 오른쪽)
InOrder(v,0);
cout << '\n';
// #3. 후위 순회(왼쪽 -> 오른쪽 -> 루트)
PostOrder(v,0);
}
// #2. 구조체 및 연결 리스트로 구현한 트리를 활용
#include <iostream>
#include <vector>
using namespace std;
struct Node
{
char Val;
Node* Left = nullptr;
Node* Right = nullptr;
};
void PreOrder(Node* cur)
{
if(cur == nullptr)
return;
cout << cur->Val;
if(cur->Left != nullptr)
PreOrder(cur->Left);
if(cur->Right != nullptr)
PreOrder(cur->Right);
}
void InOrder(Node* cur)
{
if(cur == nullptr)
return;
if(cur->Left != nullptr)
InOrder(cur->Left);
cout << cur->Val;
if(cur->Right != nullptr)
InOrder(cur->Right);
}
void PostOrder(Node* cur)
{
if(cur == nullptr)
return;
if(cur->Left != nullptr)
PostOrder(cur->Left);
if(cur->Right != nullptr)
PostOrder(cur->Right);
cout << cur->Val;
}
int main()
{
ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int N;
cin >> N;
vector<Node> Tree(26);
while(N--)
{
char Parent, Left, Right;
cin >> Parent >> Left >> Right;
int Idx = Parent-'A';
Tree[Idx].Val = Parent;
if(Left != '.')
Tree[Idx].Left = &Tree[Left-'A'];
if(Right != '.')
Tree[Idx].Right = &Tree[Right-'A'];
}
PreOrder(&Tree[0]);
cout << '\n';
InOrder(&Tree[0]);
cout << '\n';
PostOrder(&Tree[0]);
return 0;
}