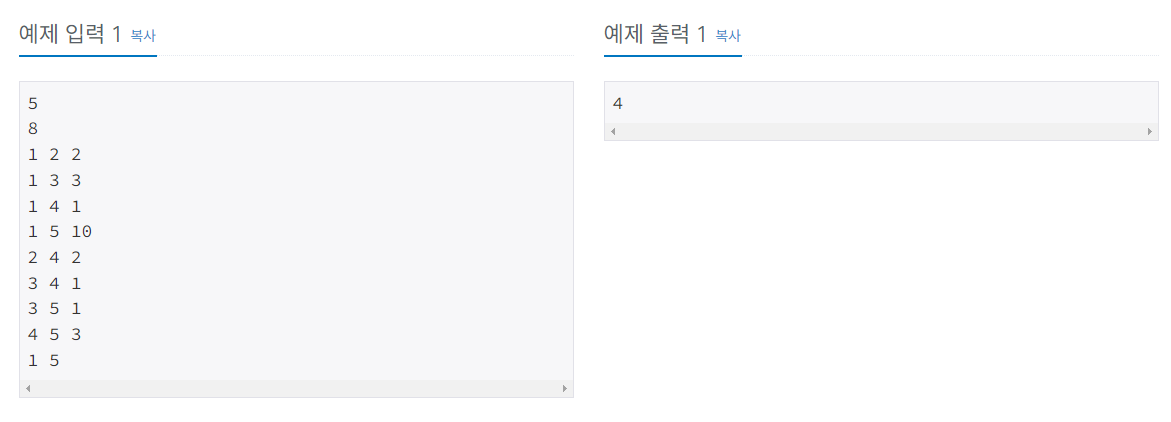
#1. 문제

#2. 풀이
1. 다익스트라 알고리즘
[알고리즘]#2_길 찾기 알고리즘
#1. 개념 1. 길 찾기 알고리즘 [정의] : 길 찾기 알고리즘은 그래프 자료구조에서 출발점에서 도착점 사이의 경로를 탐색하는 알고리즘입니다. 노드와 노드 간 연결 관계를 나타내는 간선으로 구
webddevys.tistory.com
[정의] : 다익스트라 알고리즘은 길 찾기 알고리즘 중 하나로, 양의 가중치를 갖는 그래프에서 '단일-출발 최단 경로' 알고리즘입니다.
[특징] : 다익스트라 알고리즘은 우선순위 큐를 활용해 현재 정점에서 인접한 정점들 중 우선적으로 탐색할 정점을 탐색하는데 활용하며, 각 정점은 시작 정점을 기준으로부터 최단 거리를 갱신합니다.
[성능] : 다익스트라 알고리즘의 평균 시간 복잡도는 O((E+V) log V)입니다. 그리고, 최악 시간 복잡도는 O(V² log V)입니다. 다익스트라 알고리즘은 완전 그래프에서 수행할 경우, 최악의 성능을 보여주며, 이는 간선의 개수가 (V(V-1)/2) *2 개가 되어 최종적으로 V²가 되기 때문입니다.
2. 무향 그래프 vs 방향 그래프
// #1. 무향 그래프에 대한 다익스트라 알고리즘
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;
// 그래프 자료구조의 총괄 구조체
struct Graph {
vector<vector<int>> matrix;
int NodeSize;
};
void Dijkstra(Graph* graph, int start)
{
int n = graph->matrix.size();
vector<int> distance(n, INT_MAX);
vector<bool> visited(n, false);
// #1. 출발 정점의 최단 경로 값 0으로 초기화
distance[start] = 0;
// #2. 우선 순위 큐 활용
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({ 0, start });
while (!pq.empty())
{
int cur_dist = pq.top().first;
int cur_vertex = pq.top().second;
pq.pop();
// #3. 방문 여부 체크
if (visited[cur_vertex])
continue;
visited[cur_vertex] = true;
for (int next_vertex = 0; next_vertex < n; ++next_vertex)
{
int weight = graph->matrix[cur_vertex][next_vertex];
if (weight == 0)
continue;
int new_dist = cur_dist + weight;
// #4. 최단 경로 값 수정 여부
if (new_dist <= distance[next_vertex])
{
distance[next_vertex] = new_dist;
pq.push({ new_dist, next_vertex });
}
}
}
// 결과 출력
for (int i = 0; i < n; i++) {
cout << "Distance from start to vertex " << i << ": " << distance[i] << endl;
}
}
// #2. 유향 그래프
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;
struct Edge {
int dest;
int weight;
};
void Dijkstra(vector<vector<Edge>>& graph, int start) {
int n = graph.size();
vector<int> distance(n, INT_MAX);
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
distance[start] = 0;
pq.push({0, start});
while (!pq.empty()) {
int cur_vertex = pq.top().second;
int cur_dist = pq.top().first;
pq.pop();
if (distance[cur_vertex] < cur_dist)
continue;
for (auto& edge : graph[cur_vertex]) {
int next_vertex = edge.dest;
int weight = edge.weight;
int new_dist = cur_dist + weight;
if (new_dist < distance[next_vertex]) {
distance[next_vertex] = new_dist;
pq.push({new_dist, next_vertex});
}
}
}
for (int i = 0; i < n; i++) {
cout << "Distance from start to vertex " << i << ": " << distance[i] << endl;
}
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<Edge>> graph(n);
for (int i = 0; i < m; i++) {
int start, end, weight;
cin >> start >> end >> weight;
graph[start].push_back({end, weight});
}
Dijkstra(graph, 0);
return 0;
}
[무향 그래프] : 무향 그래프의 다익스트라 알고리즘의 경우, 각 정점의 방문여부를 체크합니다. 왜냐하면, 무향 그래프의 간선은 방향성이 존재하지 않아, 한 번 방문한 정점을 다시 방문할 가능성이 있기 때문입니다.
[유향 그래프] : 유향 그래프의 다익스트라 알고리즘의 경우, 각 정점의 방문 여부를 체크하지 않습니다. 다만, 간선이 단방향임에도 불구하고, 여러 경로를 통해 한 번 방문했던 정점을 다시 방문하는 경우가 존재합니다. 따라서, 유향 그래프에 대한 다익스트라 알고리즘은 현재 정점의 최단 경로 값( cur_dist )이 이전의 최단 경로 값( distance [cur_vertex] ) 보다 클 경우, 해당 경로를 고려하지 않고 넘어갑니다.
3. 유향 그래프에 대한 다익스트라 알고리즘
- 2차원 벡터 형식의 그래프에 pair < 가중치, 도착 정점 > 형식의 항목을 활용합니다. 이는, 시작 정점과 연결된 간선의 정보들을 저장하기 위함입니다.
- 유향 그래프에 대한 다익스트라 알고리즘을 수행하고, 주어진 도착 정정의 최단 경로 값을 출력합니다.
#3. 코드
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;
int n, m;
void Dijkstra(vector<vector<pair<int, int>>> &graph, int start, int dest)
{
// 최소 거리 목록
vector<int> dist(n + 1, INT_MAX);
// 우선 순위 큐, pair< 가중치, 정점 > 에서 가중치를 기준으로 최소 힙(greater, >) 우선순위 큐 구성
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
dist[start] = 0;
pq.push({0, start});
while (!pq.empty())
{
int cur_vertex = pq.top().second;
int cur_dist = pq.top().first;
pq.pop();
// '유향 그래프' 이기 때문에, 방문여부 체크 대신 최소 거리 비용의 갱신 여부를 통해 아래 작업 수행 여부를 결정
if (dist[cur_vertex] < cur_dist)
continue;
for (auto &next : graph[cur_vertex])
{
int next_vertex = next.first;
int weight = next.second;
int new_dist = cur_dist + weight;
if (dist[next_vertex] > new_dist)
{
dist[next_vertex] = new_dist;
pq.push({new_dist, next_vertex});
}
}
}
cout << dist[dest];
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
// 2차원 벡터 형식의 그래프 구성, pair< 인접 정점, 현재 정점->인접 정점의 가중치
vector<vector<pair<int, int>>> graph(n + 1);
for (int i = 0; i < m; i++)
{
int start, dest, weight;
cin >> start >> dest >> weight;
graph[start].push_back({dest, weight});
}
int start, dest;
cin >> start >> dest;
Dijkstra(graph, start, dest);
return 0;
}
'문제 풀이 > BOJ 문제 풀이' 카테고리의 다른 글
| [BOJ알고리즘, C++]#1389_케빈 베이컨의 6단계 법칙 (1) | 2024.01.06 |
|---|---|
| [BOJ알고리즘, C++]#13549_숨바꼭질3, 우선순위 큐 (0) | 2024.01.06 |
| [BOJ알고리즘, C++]#11404_플로이드, 플로이드-워셜, 최단 경로 알고리즘, 길 찾기 알고리즘 (1) | 2024.01.05 |
| [BOJ알고리즘, C++]#1647_도시 분할 계획, MST, 최소 신장 트리, 크루스칼, 프림, 솔린 (1) | 2023.12.21 |
| [BOJ알고리즘, C++]#4386_별자리 만들기, MST, 최소 신장 트리, 크루스칼, 프림, 솔린 (1) | 2023.12.21 |
