[BOJ알고리즘, C++]#1725_히스토그램
BOJ 알고리즘 문제 풀이, 1725번 문제 "히스토그램"
C++의 STL이 제공하는 stack 컨테이너를 활용하는 문제
Overview
- 문제
- 풀이
- 코드
#1. 문제

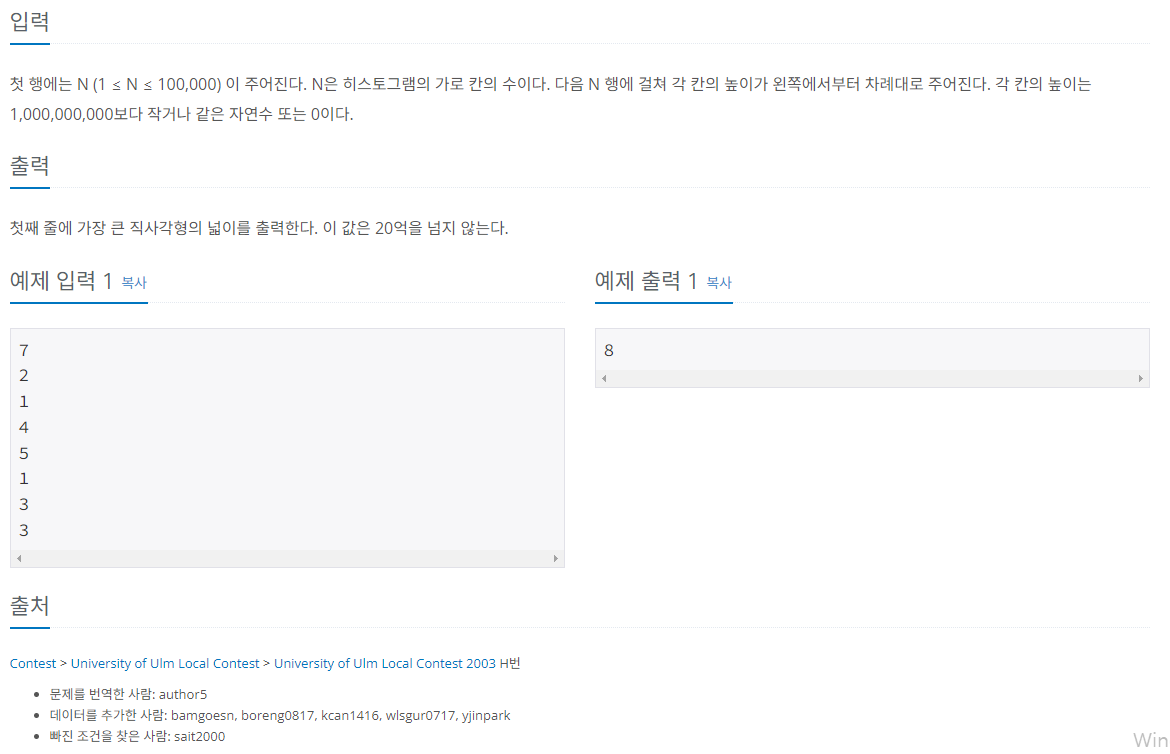
#2. 풀이
1. 스택
[자료 구조]#0_선형 자료구조
[자료 구조] #0_선형 자료구조 선형 자료구조에 대해 알아보겠습니다. Overview 개념 스택 큐 원형 큐 덱 배열 벡터 리스트 이중 연결 리스트 #0. 개념 1. 선형 자료구조? 선형 자료구조는 데이터를 일
webddevys.tistory.com
[Basic C++] #64_stack
[Basic C++] #64_stack C++에서 제공하는 stack 클래스에 대해 알아보겠습니다. Overview 개념 선언 멤버 함수 예제 #0. 개념 1. Stack C++에서 제공하는 stack은 LIFO 데이터 구조를 구현하는 STL 컨테이너입니다. s
webddevys.tistory.com
Details
- 스택은 LIFO(후입선출) 방식으로 동작하는 선형 자료구조입니다.
- 스택은 같은 구조와 같은 크기의 데이터를 정해진 한 방향으로만 삽입/삭제가 가능한 자료구조입니다.
2. 직사각형 넓이를 구하는 시점
- 먼저, 히스토그램의 각 높이를 저장하는 배열을 정의합니다.
- 현재 막대가 stack의 top의 높이보다 작을 경우, 직사각형 넓이를 계산합니다. 왜냐하면, 우리는 먼저 직사각형의 넓이가 최대가 될 수 있도록 width(밑변의 길이이자 현재 누적된 히스토그램 막대의 개수)가 최대가 될 수 있도록 해야 합니다. 따라서, 현재 막대의 높이가 stack.top의 높이보다 크다면, 더 이상 직사각형의 밑변의 길이를 추가할 수 없게 되어, 현재까지 누적되어 있는 막대들을 통해 최대 직사각형 넓이를 찾아야 합니다. 돌아가서, 현재 막대의 높이가 stack의 top의 높이보다 작을 경우, stack의 top 값을 꺼내어 이 막대의 높이와 width 값( i - s.top() - 1 )을 통해 직사각형 넓이를 구하고 현재 최대 직사각형 넓이를 갱신합니다.
- 그리고, 현재 막대의 인덱스를 stack에 push 합니다.
- 위 과정을 반복하며, 최대 직사각형 넓이를 찾습니다.
- 주의할 점은 마지막 막대가 stack에 삽입되고 다음 차례에 삽입할 막대가 더 이상 남아 있지 않을 경우, 마지막 막대를 포함해 최대 직사각형 넓이를 구하는 작업이 생략될 수 있습니다. 이를 방지하기 위해, N개의 히스토 그램이 있다면, 배열을 여유있게 할당받고 탐색 작업을 N+1번 수행하도록 코드를 작성합니다.
#3. 코드
#include <iostream>
#include <stack>
#include <algorithm>
using namespace std;
int N, ans, h[100002];
stack<int> s;
int main()
{
ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin >> N;
for(int i=1; i<=N; i++)
{
cin >> h[i];
}
s.push(0);
for(int i=1; i<=N+1; i++)
{
while(!s.empty() && h[s.top()] > h[i])
{
int cur = s.top();
s.pop();
int width = i - s.top() - 1;
ans = max(ans, h[cur] * width);
}
s.push(i);
}
cout << ans;
return 0;
}
'문제 풀이 > BOJ 문제 풀이' 카테고리의 다른 글
| [BOJ알고리즘, C++]#1655_가운데를 말해요, 우선순위 큐, 최소 힙, 최대 힙 (0) | 2023.11.23 |
|---|---|
| [BOJ알고리즘, C++]#3015_오아시스 재결합, 스택 (0) | 2023.09.29 |
| [BOJ알고리즘, C++]#17299_오등큰수, 스택, unordered_map (0) | 2023.09.25 |
| [BOJ알고리즘, C++]#17298_오큰수, 스택 (0) | 2023.09.25 |
| [BOJ알고리즘, C++]#9935_문자열 폭발, 문자열 (0) | 2023.09.25 |
