[기술 질문] #18_알고리즘 복잡도
알고리즘의 복잡도에 대해 알아보겠습니다.
Overview
- 개념
- 시간 복잡도
- 공간 복잡도
#0. 개념
1. 복잡도
- 알고리즘의 복잡도는 알고리즘의 입력 크기와 연산 횟수 사이의 관계를 나타내는 함수입니다.
- 보통 시간 복잡도와 공간 복잡도로 나누어져 있습니다.
#1. 시간 복잡도
1. 개념
- 시간 복잡도는 알고리즘이 실행되는 동안 수행하는 기본적인 연산 횟수를 입력 크기와 연관시켜 분석하는 것입니다. 결과적으로, 입력 크기에 따라서 알고리즘의 실행 시간이 어떻게 변화하는지 나타내며, 알고리즘의 효율성과 성능을 평가하는 중요한 지표 중 하나입니다.
- Big-O 표기법은 알고리즘의 시간 복잡도를 점근적으로 표기하는 방법입니다. 즉, 알고리즘의 입력의 크기가 충분히 커질 때, 알고리즘의 실행 시간의 상한을 나타내는 함수를 사용하여 알고리즘의 성능을 평가합니다. 이때, 실행 시간의 상한이란 알고리즘의 입력 크기가 최대일 경우를 가정해 알고리즘이 수행하는 데 걸리는 시간의 상한을 나타냅니다.
2. Big-O 표기법
- 최악 시간 복잡도 : 최악 시간 복잡도는 알고리즘의 입력 크기가 가장 큰 경우를 가정해 알고리즘이 수행하는데 걸리는 시간의 상한을 나타냅니다. 알고리즘의 성능을 평가하는 가장 일반적인 방법입니다.
- 최선 시간 복잡도 : 최선 시간 복잡도는 알고리즘의 입력 크기가 가장 작을 경우를 가정해 알고리즘이 수행하는데 걸리는 시간의 하한을 나타냅니다.
- 평균 시간 복잡도 : 평균 시간 복잡도는 알고리즘의 입력 크기의 모든 경우에 대한 평균 시간 복잡도를 나타냅니다.
3. Big-O 표기법 그래프
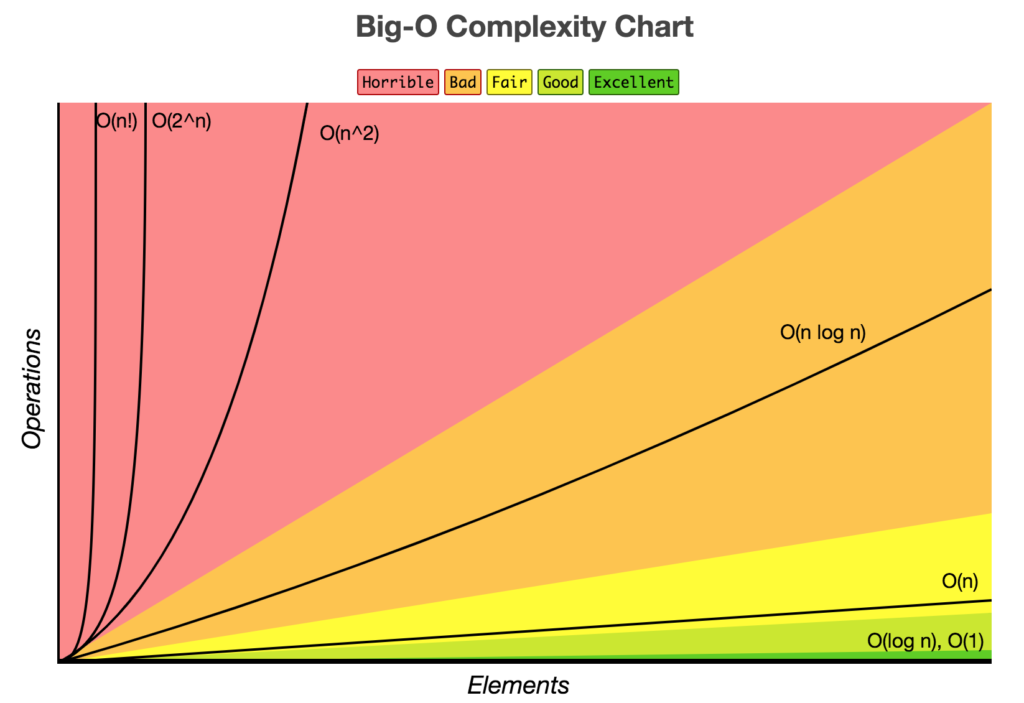
Details
- O(1), 상수 시간 알고리즘 : 상수 시간 알고리즘은 입력 크기와 상관 없이 일정한 실행 시간을 갖는 알고리즘입니다. 인덱스를 활용해 배열에 Random Access를 하는 작업이 상수 시간의 성능을 보여줍니다.
- O(log n), 로그 시간 알고리즘 : 로그 시간 알고리즘은 입력 크기가 n일때, 실행 시간이 log n과 비례하는 알고리즘입니다. 주로 이진 탐색과 분할 정복 알고리즘이 로그 시간의 성능을 보여줍니다.
- O(n), 선형 시간 알고리즘 : 선형 시간 알고리즘은 입력 크기가 n일때, 실행 시간이 n과 비례하는 알고리즘입니다. 주로, 배열의 순회, 리스트 내 검색 알고리즘 등이 선형 시간 알고리즘입니다.
- O(n log n), 로그 선형 시간 알고리즘 : 로그 선형 시간 알고리즘은 입력 크기가 n일 때, 실행 시간이 n log n과 비례하는 알고리즘입니다. 주로, 병합 정렬과 퀵 정렬 등이 로그 선형 시간 알고리즘입니다.
- O(n^2), 이차 시간 알고리즘 : 이차 시간 알고리즘은 입력 크기가 n일 때, 실행 시간이 n^2와 비례하는 알고리즘입니다. 주로, 이중 for문을 사용하는 알고리즘(버블 정렬)등이 해당됩니다.
- O(2^n), 지수 시간 알고리즘 : 지수 시간 알고리즘은 입력 크기가 n일 때, 실행 시간이 2^n과 비례하는 알고리즘입니다. 주로 부분 집합 생성, 완전 탐색 등이 지수 시간 알고리즘입니다.
4. 예제-1
void quickSort(vector<int>& arr, int left, int right) {
int i = left, j = right;
int pivot = arr[(left + right) / 2];
// 분할
while (i <= j) {
while (arr[i] < pivot) i++;
while (arr[j] > pivot) j--;
if (i <= j) {
swap(arr[i], arr[j]);
i++;
j--;
}
};
// 재귀 호출
if (left < j)
quickSort(arr, left, j);
if (i < right)
quickSort(arr, i, right);
}
Details
- 위 코드는 "퀵 정렬"을 수행하는 함수를 구현합니다.
- 퀵 정렬은 분할 정복 알고리즘으로, 피봇 값을 정해 피봇을 기준으로 왼쪽은 피봇과 같거나 작은 수로, 오른쪽은 피봇과 같거나 큰 수로 정렬 하고, 피봇 기준으로 왼쪽 부분 배열과 오른쪽 부분 배열에 대해 재귀 호출하는 정렬 알고리즘입니다.
- 자세한 내용은 추후에 살펴보겠지만, 퀵 정렬은 이미 정렬되어 있는 배열의 경우 O(n^2)의 최악의 성능을 보여줍니다. 알고리즘 작성 방법에 따라 다르겠지만, pivot 값을 항상 배열의 마지막 인덱스의 항목으로 설정하는 퀵 정렬 알고리즘의 경우 오른쪽 부분 배열과 왼쪽 부분 배열이 균등하게 분할되지 않아 최악의 성능을 보여줍니다.
#2. 공간 복잡도
1. 개념
- 공간 복잡도는 알고리즘이 실행되는 동안에 필요한 메모리 공간의 양을 나타냅니다.
- 일반적으로, 공간 복잡도는 고정 공간, 입력 공간, 출력 공간, 그리고 추가 공간을 고려합니다.
- 고정 공간은 알고리즘이 실행되는 동안 항상 사용되는 공간(eg, 코드를 저장하는 공간)
- 입력 공간은 말 그대로 알고리즘이 실행될 때, 입력 데이터를 저장하는 공간을 의미합니다.
- 출력 공간은 말 그대로 알고리즘의 실행 결과를 저장하는 공간을 의미합니다.
- 추가 공간은 알고리즘이 실행될 때, 추가적으로 사용되는 공간(임시 변수, 스택, 배열 등)을 의미합니다.
'언어 > 기술 질문' 카테고리의 다른 글
| [기술 질문]#17_Lambda (0) | 2023.03.27 |
|---|---|
| [기술 질문]#16_RTTI, 런타임 타입 정보 (0) | 2023.03.22 |
| [기술 질문]#15_가상 함수 (0) | 2023.03.20 |
| [기술 질문]#14_템플릿, Template (0) | 2023.03.12 |
| [기술 질문]#13_6가지 디폴트 멤버 메서드 (0) | 2023.03.05 |
