문제 풀이/Programmers 문제 풀이
[Programmers_C++]#Level2_멀리 뛰기, dp, 동적 프로그래밍
Hardii2
2023. 12. 24. 15:33
#1. 문제

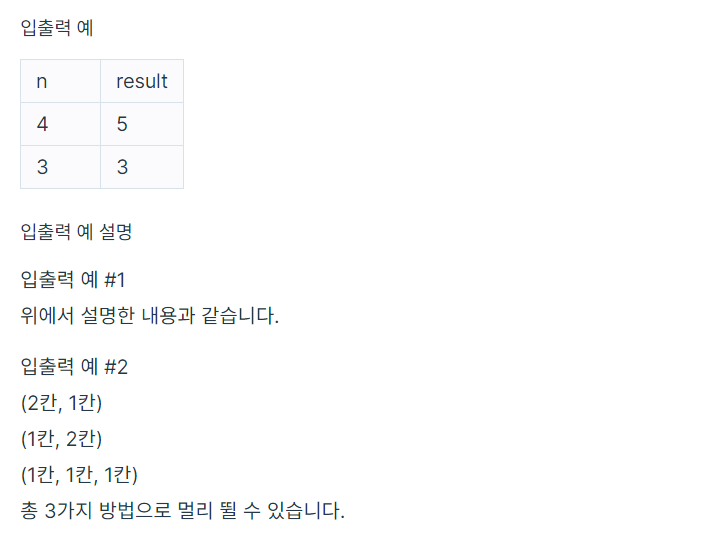
#2. 풀이
1. 동적 계획법
[알고리즘]#5_동적 계획법
[알고리즘]#5_동적 계획법 동적 계획 알고리즘에 대해 알아보겠습니다. Overview 개념 예제 #0. 개념 1. 동적 계획법(Dynamic Programming) 동적 계획법은 최적화 문제를 해결하는 데 사용되는 알고리즘 디
webddevys.tistory.com
Details
'동적 계획법'은 최적화 알고리즘 디자인 기법 중 하나입니다. 동적 계획법은 입력 크기에 따라서 중복되는 하위 문제를 재귀적으로 해결하고, 이 결과 값을 저장하고 기억하는 것으로 중복 계산을 방지해 최적를 수행하여 효율적으로 최적해를 찾아냅니다.
2. DFS 활용(x) -> DP 활용(o)
- 해당 문제의 최적해를 찾기 위해 DFS를 활용할 경우, 시간 초과 문제가 발생합니다.
- Memoization을 통해 이전 단계의 경우의 수를 기억하며 동적 계획법을 구현합니다, DP[i] = DP[i-1] + DP[i-2]
#3. 코드
1. DFS 활용, 실패 코드
// 오답 코드
#include <string>
#include <vector>
using namespace std;
void dfs(int cnt, const int &maxCnt, int &answer)
{
if (cnt == maxCnt)
{
answer++;
return;
}
else if (cnt > maxCnt)
{
return;
}
else
{
if (maxCnt - cnt < 2)
{
dfs(cnt + 1, maxCnt, answer);
}
else
{
dfs(cnt + 1, maxCnt, answer);
dfs(cnt + 2, maxCnt, answer);
}
}
}
long long solution(int n)
{
long long answer = 0;
dfs(1, n, answer);
dfs(2, n, answer);
return answer % 1234567;
}
2. DP 활용, 정답 코드
// 정답 코드
#include <string>
#include <vector>
using namespace std;
long long solution(int n)
{
long long answer = 0;
vector<long long> dp(2001, 0);
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; ++i)
{
dp[i] = (dp[i - 1] + dp[i - 2]) % 1234567;
}
return dp[n];
}