문제 풀이/BOJ 문제 풀이
[BOJ알고리즘, C++]#24479_알고리즘 수업 - 깊이 우선 탐색 1, DFS, 재귀 DFS, 스택 DFS
Hardii2
2023. 12. 14. 00:35
#1. 문제
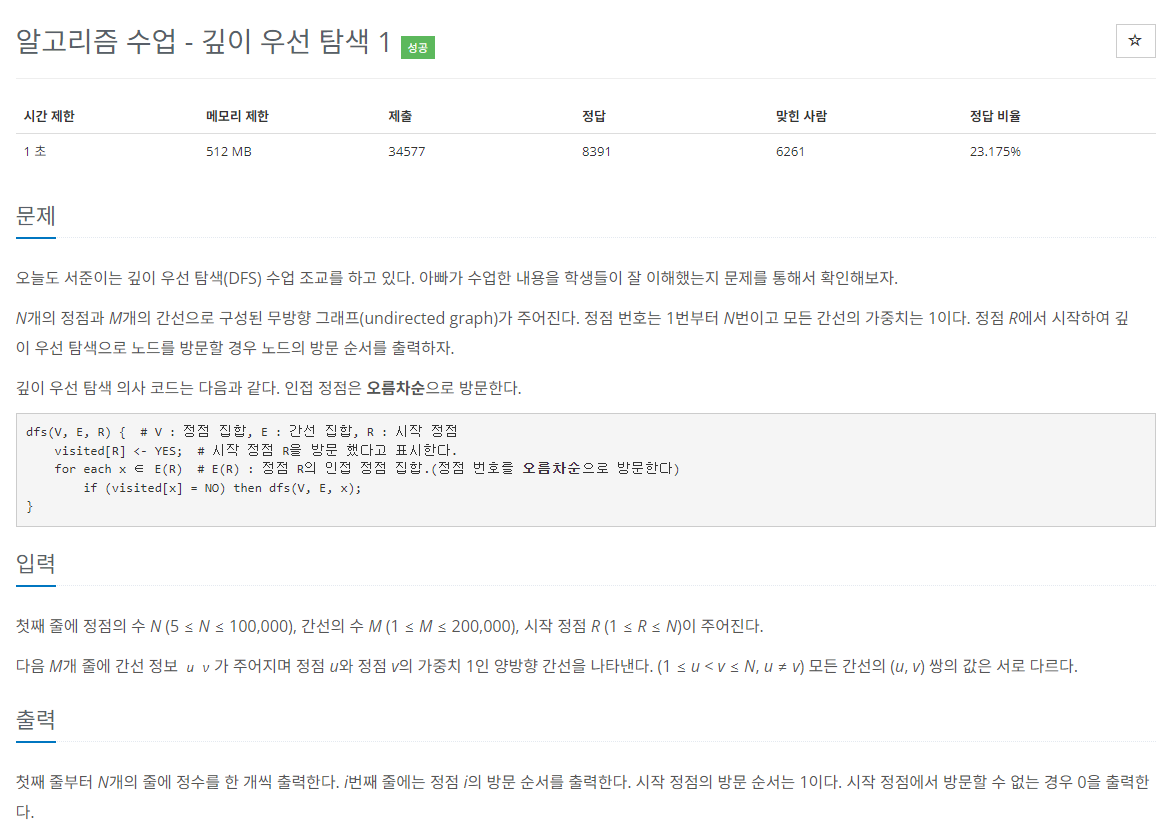
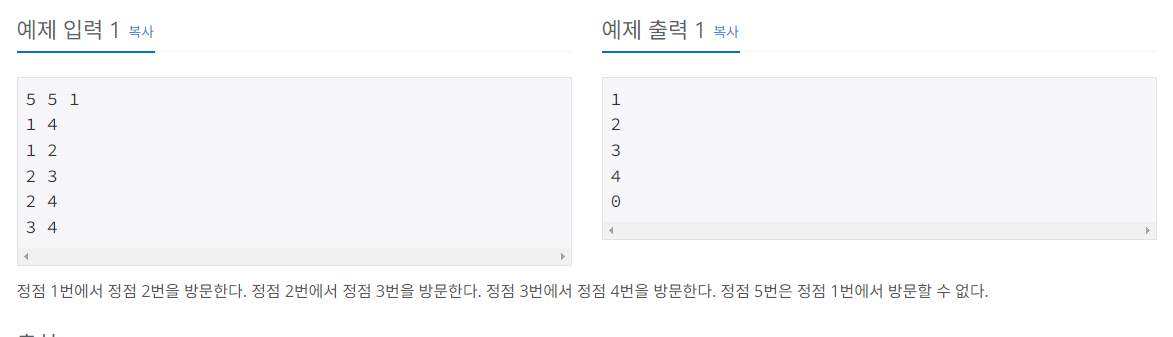
#2. 풀이
1. DFS(깊이 우선 탐색)
[자료구조]#6_그래프
#0. 개념 1. 그래프? [정의] : 그래프는 노드와 간선들의 집합으로 이루어진 비 선형 자료구조입니다. 그래프의 노드들은 간선을 통해 연결되어 일종의 네트워크를 형성합니다. 그래프는 노드와
webddevys.tistory.com
- [정의] : 깊이 우선 탐색은 그래프의 모든 정점을 탐색하는 방법 중 하나입니다.
- [특징] : 깊이 우선 탐색은 한 노드에서 시작해 그래프의 깊은 부분을 우선적으로 탐색하는 방법입니다.
- [동작 방식] : DFS는 일반적으로 재귀적으로 호출하는 방법과 스택을 활용하는 방법이 있습니다.
- 재귀적 호출
- 스택
2. 정점을 방문할 때마다 순서를 기록하자
- 먼저, 주어진 간선 정보를 저장하고, 인접 정점들을 오름차순 정렬해 줍니다.
- DFS 호출 후 각 정점 방문 시 해당 정점을 방문한 순서를 기억합니다.
#3. 코드
1. 재귀 DFS
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
int N, M, R;
// 재귀를 활용한 DFS 구현
void DFS(int cur, int& curSeq, vector<int>& seq, vector<vector<int>>& graph, vector<bool>& visited)
{
// 방문 여부 체크
visited[cur] = true;
// 현재 정점의 방문 순서 업데이트
seq[cur] = curSeq++;
for(int next=0; next<(int)graph[cur].size(); ++next)
{
int nextNode = graph[cur][next];
if(!visited[nextNode])
{
// DFS 재귀 호출
DFS(nextNode, curSeq, seq, graph, visited);
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> N >> M >> R;
// 2차원 벡터 형식의 그래프
vector<vector<int>> graph(N+1);
// 방문 순서, 0으로 초기화
vector<int> seq(N+1, 0);
// 방문 여부
vector<bool> visited(N+1, false);
// 현재 순서
int curSeq = 1;
// #2. 그래프 구성
for(int i=0; i<M; ++i)
{
int node1, node2;
cin >> node1 >> node2;
graph[node1].push_back(node2);
graph[node2].push_back(node1);
}
// #4. 각 노드 별 인접 정점을 오름차순 정렬
for(auto& next : graph)
{
sort(begin(next), end(next));
}
// #5. DFS 수행
DFS(R, curSeq, seq, graph, visited);
// #6. 결과 출력
for(int i=1; i<= N; ++i)
{
cout << seq[i] << '\n';
}
return 0;
}
2. 스택을 활용한 DFS
#include <iostream>
#include <vector>
#include <string>
#include <stack>
#include <algorithm>
using namespace std;
int N, M, R;
// 재귀를 활용한 DFS 구현
void DFS(int start, vector<vector<int>>& graph)
{
// 방문 순서, 0으로 초기화
vector<int> seq(N+1, 0);
// 방문 여부, false로 초기화
vector<bool> visited(N+1, false);
// 스택 선언
stack<int> s;
// 현재 정점의 순서
int curSeq = 1;
// 시작 노드 스택에 삽입
s.push(start);
// 스택 순회
while(!s.empty())
{
int cur = s.top();
s.pop();
if(visited[cur])
continue;
visited[cur] = true;
seq[cur] = curSeq++;
// '오름차순' 정렬되어 있기 때문에, 역순으로 순회하며 stack에 삽입
for(int i=graph[cur].size()-1; i>= 0; --i)
{
// 방문 여부 체크
if(!visited[graph[cur][i]])
{
// 스택에 삽입
s.push(graph[cur][i]);
}
}
}
// 정답 출력
for(int i=1; i<=N; ++i)
cout << seq[i] << '\n';
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> N >> M >> R;
// #1. 2차원 벡터 형식의 그래프
vector<vector<int>> graph(N+1);
// #2. 그래프 구성
for(int i=0; i<M; ++i)
{
int node1, node2;
cin >> node1 >> node2;
graph[node1].push_back(node2);
graph[node2].push_back(node1);
}
// #3. 각 노드 별 인접 정점을 오름차순 정렬
for(auto& next : graph)
{
sort(begin(next), end(next));
}
// #4. DFS 수행
DFS(R, graph);
return 0;
}