문제 풀이/BOJ 문제 풀이
[BOJ알고리즘, C++]#15650_N과 M(2), 백 트래킹, 조합
Hardii2
2023. 7. 27. 20:59
[BOJ알고리즘, C++]#15650_N과 M(2)
BOJ 알고리즘 문제 풀이, 15650문제 N과 M(2)
조합 문제를 백 트래킹을 활용해 해결하는 방법에 대해 알아보겠습니다.
Overview
- 문제
- 풀이
- 코드
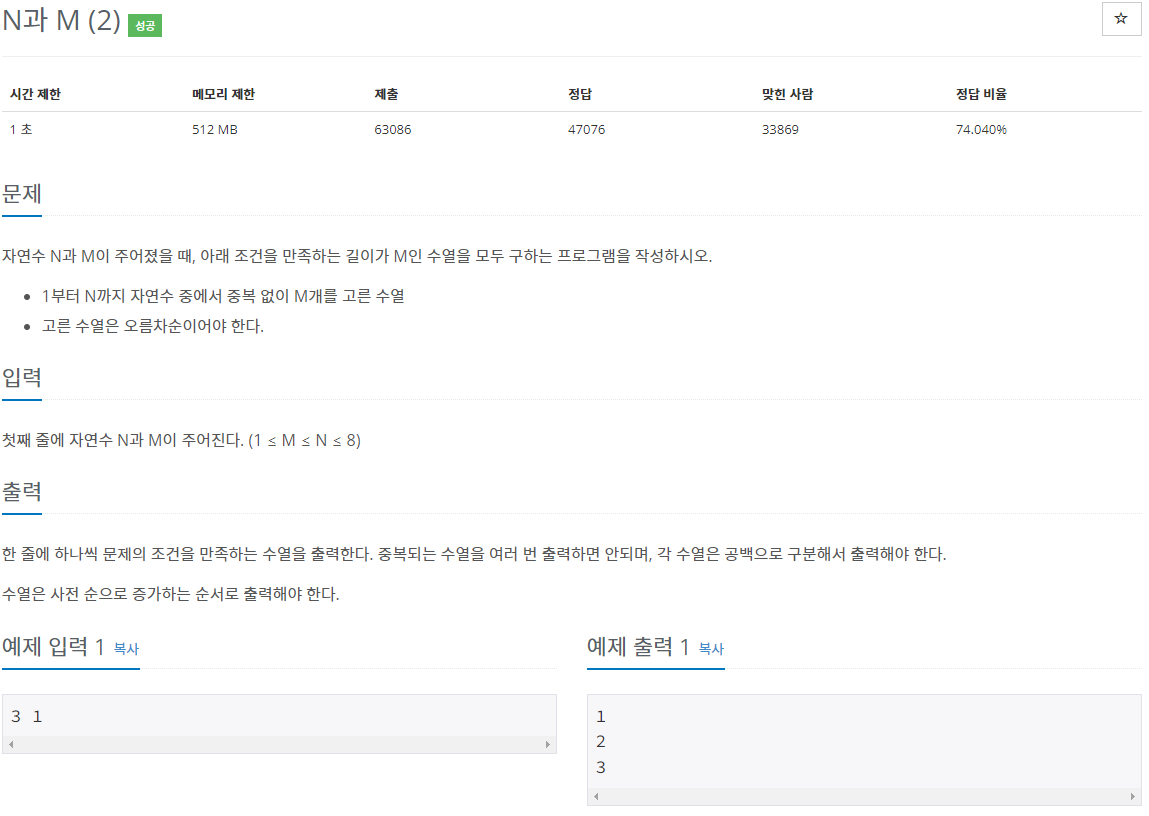
#0. 문제

#1. 풀이
1. 백 트래킹
// 링크
- 조합 문제는 백 트래킹 알고리즘을 활용하는 대표적인 문제 중 하나입니다.
- 백 트래킹 알고리즘은 문제 해결을 위해 여러 후보 해결책들을 점진적으로 탐색하며, 현재 선택한 경로가 해결책으로 이어질 수 없다고 판단되면, 이전 단계로 돌아가 다른 경로에 대한 탐색을 시도하는 알고리즘입니다. 이를 통해, 효율적으로 문제의 모든 가능한 후보 해결책들을 탐색할 수 있습니다.
2. 조합
[확률과 통계]#2 조합, nCr
[확률과 통계]#2 조합, nCr 확률과 통계 과목의 "순열과 조합"에 대해 공부합니다. Overview 조합과 순열의 차이점 조합의 성질 같은 것이 있는 순열 vs 조합 중복 조합 조합과 순열의 차이점 1. 조합? D
webddevys.tistory.com
- 조합(nCm)은 서로 다른 n개 중에서 순서 상관없이 m개를 선택하는 것입니다.
- 이때, 우리가 주목할 점은 "순서"입니다. 조합의 경우, "1, 2"와 "2, 1"은 동일한 경우로 취급합니다.
#2. 코드
1. 코드
#include <iostream>
#include <vector>
using namespace std;
int N, M;
vector<int> ans;
void dfs(int depth, int start)
{
if(depth == M)
{
for(int i=0 ;i<M; i++)
{
cout << ans[i] << ' ';
}
cout << '\n';
return;
}
for(int i=start; i<=N; i++)
{
ans.push_back(i);
dfs(depth+1, i+1);
ans.pop_back();
}
}
int main()
{
ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin >> N >> M;
dfs(0, 1);
return 0;
}