언어/기술 질문
[기술 질문]#9_부동 소수점, float
Hardii2
2023. 2. 18. 00:17
[기술 질문] #9_부동 소수점
float 자료형과 부동 소수점에 대해 알아보겠습니다.
Overview
- 고정 소수점
- 부동 소수점
- 오차 발생의 이유
- 무한과 NaN
#0. 고정 소수점
1. 개념

- 컴퓨터에서 실수를 표현하는 두 가지 방식 중 "고정 소수점" 방식은 소수부의 자릿수를 미리 정하여, 고정된 자릿수의 소수만 표현하는 것입니다.
- 가장 왼쪽의 1Bit는 부호를 표현하고, 나머지 31Bit를 정수부와 소수부로 표현합니다.
- 소수부는 점을 기준으로 순서대로 채우며, 나머지 Bit는 0으로 채워줍니다.
- 고정 소수점 방식의 장점은 구현의 편리함입니다.
- 고정 소수점 방식의 단점은 비트 수 대비 표현 가능한 수의 범위와 정밀도가 낮기 때문에 실수 표현을 다루는 범용 시스템에서 사용하지 않고, 높은 정밀도를 필요로 하지 않는 소규모 시스템에서 사용합니다.
#1. 부동 소수점
1. 개념
- "고정 소수점"은 한정된 비트에 정수와 소수를 분할해 배치하기 때문에 표현 범위가 비교적 한정되어 있습니다.
- 부동 소수점은 실수를 컴퓨터 상에서 근사하여 표현할 때 소수점의 위치를 고정하지 않고 그 위치를 나타내는 수를 따로 적습니다. 유효 숫자는 가수로, 소수점의 위치를 표현하는 지수로 나누어 표현하는 방식입니다.
- "부동 소수점"은 아주 작은 수, 아주 큰 수, 그리고 무한과 NaN을 표현합니다.
- 간단한 예제를 통해 부동 소수점 표현 방식의 원리를 알아보겠습니다.
2. 소수점의 2진 변환

Details
- 먼저, 실수를 2진법으로 변화는 것부터 시작합니다.
- 정수, 즉 "-9.6875" 중 9는 1001로 간단하게 변환이 가능합니다.
- 소수, 즉 "-9.6875" 중 6875는 우리가 아는 2진 변환을 반대로 적용하면 됩니다.
- 기존의 2진 변환은 해당 숫자를 2로 나누어 나머지를 취하는 반면, 소수의 2진 변환은 2를 곱해주어 나오는 결과 값의 정수 부분을 취합니다.
- 최종적으로, -1001.1011(2)가 -9.6875의 2진 변환의 결과입니다.
3. 지수 표기법

-1001.1011(2) = -1.0011011(가수부) x 2³(지수부)
- -1001.1011(2)를 그대로 저장하면 고정 소수점 방식과 다를 게 없죠.
- -1001.1011(2)를 부동 소수점 표현 방식으로 저장하기 위해 우리는 정규화 과정을 통해 "지수 표기법"을 통해 실수를 표현합니다.
- -1001.1011(2)를 정규화하면, -1.0011011 x 2³가 됩니다.
- 이때, "0011011"은 가수부, "3"은 지수부라고 부릅니다.
- IEEE754 기준 float형(32Bit)은 [ 부호부 1Bit | 지수부 8Bit | 가수부 23Bit ]
- IEEE754 기준 double형(64Bit)은 [ 부호부 1Bit | 지수부 11Bit | 가수부 52Bit ]
- float형을 기준으로 사용되는 지수는 -127 ~ 128입니다.
- 이때 주의할 점은 [ 0000,0000 ]은 -127을 나타내고, [ 0000,0001 ]은 -126을 나타냅니다. 이를 Bias 표현법이라고 합니다.
3. 예제, float형의 -9.6875
-9.6875 = [ 부호부 = 음수 | 지수부 = 3 | 가수부 = 0011011 ]
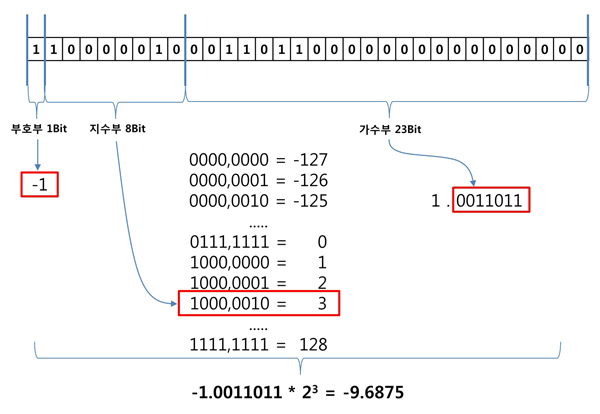
- Bias 표기법에 의하면 지수부, 3은 -127을 첫 번째 기준으로 130번째가 됩니다. 따라서, 130을 2진수로 표현하여 [ 1000,0010 ]이 됩니다.
4. 가장 작은 수
- 부동 소수점으로 표현가능한 '정규화된 형태'의 가장 작은 수는 1x2^-127 입니다. 이 수는 충분히 작은 숫자지만, 0과 가장 근사한 더 작은 숫자들을 표현하기에 한계가 분명합니다. 따라서, IEEE 754는 이러한 "언더 플로우" 문제를 해결하기위해 몇 가지 규칙을 정했습니다.
1. IEEE 754 기준, 지수부가 모두 0일 경우, 유효 숫자의 정수부는 1에서 0으로 변경한다.
2. IEEE 754 기준, 지수부가 모두 0일 경우, 위 작업을 수행하고 지수부는 -127이 아닌, -126으로 설정한다.
Details
- IEEE 754는 지수부(4bit)가 모두 0일 경우 유효 숫자의 정수부를 1에서 0으로 변경하는 '정규화된 형태의 수'에서 '비 정규화된' 형태의 수로 변경합니다. 이러한 작업은 '언더 플로우'를 처리하기에 유용한 방법입니다. 예를 들면, 1x2^-127 보다 0.0000,0000...1 x 2^-126 이 더욱 0과 근사한 값을 표현할 수 있게 되죠.
- IEEE 754는 지수부가 모두 0일 경우, 위 작업을 수행하고, 지수부를 -127이 아닌, -126으로 설정합니다. 만약, 지수부를 그대로 -127로 남겨둘 경우, 지수부가 모두 0인 1x2^-127은 위와 같은 '비 정규화된' 형태의 수로 변경되어, 1x2^-127은 표현할 수 없는 수가 되버립니다. 따라서, 1x2^-126의 경우, 지수부가 0001이 되어 '언더 플로우' 처리 조건과 합치하지 않아 문제가 발생하지 않기 때문에, -127 대신 -126으로 지수부를 설정합니다.
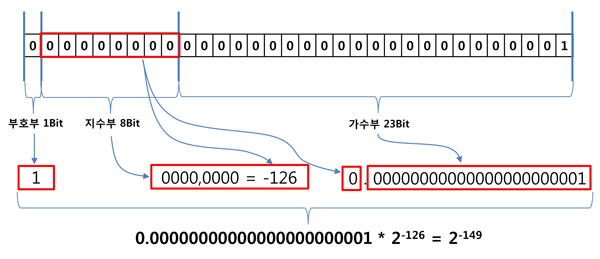
가장 작은 수 = 1 X 2^-127 (X) -> 유효 숫자의 정수부 1, 가수부 모두 0, 지수부 -127
가장 작은 수 = 0.0000...0001 X 2^-126 (O) -> 유효 숫자의 정수부 0, 가수부 마지막만 1, 지수부 -126
Details
- 최종적으로, IEEE754는 0.0000...1 x 2^-126( 1/2^149 )을 최소 값으로 규정하는 '언더 플로우' 처리를 통해, 1x2^-127 보다 0과 근사한 더 작은 값들을 세밀하게 표현 가능토록 했습니다.
- double의 경우도 마찬가지입니다. 가수부에게 할당된 Bit 수에 127만 126만 더해주면 1074가 되어, 결국 2^-1074 가 최소 값이 됩니다.
#2. 오차 발생의 이유 및 허용 범위
1. 부동 소수점 표현의 한계
- 부동 소수점 방식은 표현의 한계가 존재합니다.
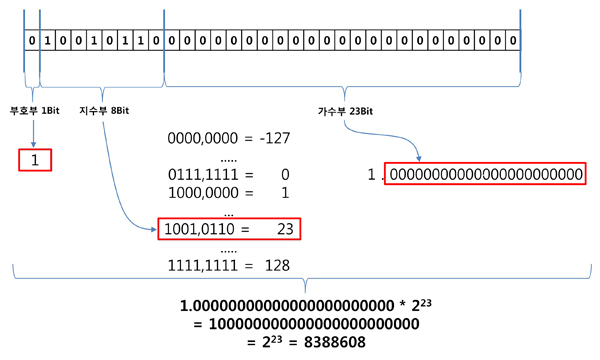
- 위에서 살펴봤듯이, IEEE754 기준 float 형의 가수부가 갖는 최대 크기는 23Bit입니다.
- 만약, 지수부가 23 이상일 경우에는 가수부에 상관없이 소수점이 오른쪽으로 23자리 이상 이동하게 되므로, 실수의 소수점 밑에 있는 숫자들을 표현할 수 없게 됩니다!
- 따라서, float 형이 표현할 수 있는 최대 값은 8,388,608(10)입니다.
- float의 실수가 8,388,608 이상으로 커질 경우, 가장 근사한 정 수값을 선택합니다.
- float형 사용 시 숫자가 커질수록 해당 오차도 같이 커지게 되며, 지수가 23 이상일 때는 더 이상 소수점을 표현할 수 없고, 지수가 24 이상일 때는 짝수 정수만을 표현할 수 있습니다. 25 이상일 때는 오직 4의 배수만 표현할 수 있습니다.
2. 예제, 지수부가 25이상일 경우의 오차
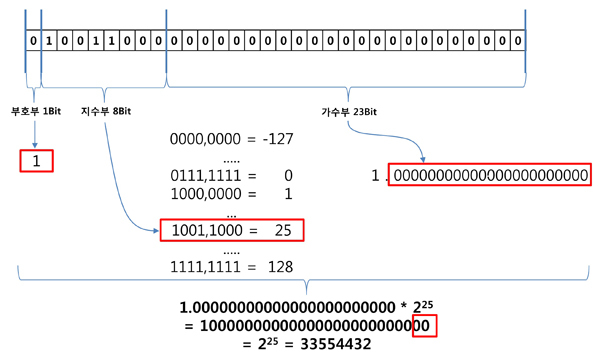
- 위 그림을 살펴보면, 지수부가 25이며 가수부는 모두 0입니다.
- float형의 가수부가 표현할 수 있는 최대 크기는 23Bit이며, 유효숫자의 소수점을 오른쪽으로 25자리 이동하면 무조건 마지막 두 자리는 0으로 채워집니다.
- 2진수에서 두 자리는 4(10)를 의미하므로, 지수부가 25 이상이면 float형이 표현할 수 있는 정수는 모두 4의 배수가 됩니다.
- 따라서, 정수 단위의 큰 수를 다룰 때 float 혹은 double을 사용하는 것이 아니라, long long(64Bit)을 활용해야겠죠!
#3. 무한과 NaN(Not A Number)
1. 부동 소수점의 무한
무한 = [ 0111, 1111, 1000, 0000, 0000, 0000, 0000, 0000]
- 부동 소수점의 무한은 지수부(8Bit)를 모두 1로 채우고, 가수부를 모두 0으로 채운 상태를 뜻합니다.
- 지수부(8Bit)의 범위는 -126 ~ 128이므로, 지수부의 128은 무한을 의미합니다. 동시에, 실제 지수의 범위는 무한을 제외하면 -126~127까지입니다.
- 이때, 양의 무한과 음의 무한으로 다시 나누어지는데, 구분 방법은 당연하게도 부호(1Bit)입니다.
2. 부동 소수점의 NaN(Not A Number)
- 부동 소수점의 NaN(미정의 결과 | 값이 없는 상태)은 지수부(8Bit)를 모두 1로 채우고, 가수부의 어느 한 비트라도 1인 상태를 의미합니다.